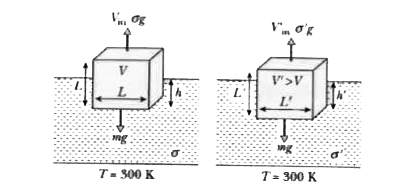
Text Solution
Verified by Experts
Topper's Solved these Questions
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
RESNICK AND HALLIDAY|Exercise CHECKPOINT|8 VideosTEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
RESNICK AND HALLIDAY|Exercise PROBLEMS|24 VideosRIGID BODY DYNAMICS-II
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (Integer Type)|2 VideosTHE FIRST LAW OF THERMODYNAMICS
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS ( INTEGER TYPE )|3 Videos
Similar Questions
Explore conceptually related problems
RESNICK AND HALLIDAY-TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION -PRACTICE QUETIONS (Integer Type)
- An aluminium cube of side 20cm floats in mercury. How much farther wil...
Text Solution
|
- A pendulum clock loses 12s a day if the temperature is 40^@C and gains...
Text Solution
|
- The length of the steel rod which would have the same difference in le...
Text Solution
|
- Find the approximate length of the Golden Gate bridge if it is known t...
Text Solution
|
- The brass bar and the alumiumn bar in the drawing are each attached to...
Text Solution
|