The cycle of a petrol engine can be approximated by an Otto cycle (Fig. 21-20a). 1`to` 2 and 3 `to ` 4 are adiabatic compression and expansion, respectively, 2 `to `3 and `4 to `1 are constant-volume processes. Treat the working medium as an ideal gas with constant `gamma =C_p //C_v `, Compute the efficiency of this cycle for g = 1.4 and compression ratio, `r=V_i //V_f =10`

Explanation

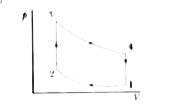
We can see from the p-V graph (Fig. 21-20b) that it is a cyclic process as the working medium returns to its initial state. We can see from the p-V graph that in the process 3`to ` 4, the engine is doing positive work on the surroundings and in 1 `to ` 2, it is doing negative work as the gas is compressed. In other two processes, 2`to ` 3 and 4 `to ` 1, work done is zero, as `Delta `V =0.
The efficiency of a cyclic process is given by `epsi = W//Q_1`, where W is the work done by the cycle and `Q_1` is the amount of heat absorbed by the working medium in this case, gas). Because the working medium returns to its initial state `W =Q_1 -Q_2`, where` Q_2` is the amount of heat transferred from the gas. Therefore,
`epsi =(Q_1 -Q_2 )/(Q_1) =1 -(Q_2)/(Q_1)`
As the processes 1`to ` 2 and 3 `to `4 are adiabatic, heat transfer can take place only during the 2`to` 3 and 1 `to `4 stages.

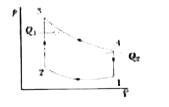
Calculations: Let us calculate `Q_1 ` and `Q_2` Since both processes are occurring at a constant volume (Fig. 21-20b), we may write
` Q_1 = int _(2)^3 dQ = C_v int _(2)^(3) dT =C_v (T_3 -T_2)`
` Q_2 = C_V int_(4)^(3) dT =- C_v (T_1 -T_4) =C_v (T_4 -T_1)`
and `(Q_2)/(Q_1) =(T_4-T_1 )/(T_3-T_2)`
We know that for an adiabatic process
` pV^( gamma)` = constant or `TV^(r-1)`= constant
So `_1 V_(i )^( gamma -1) =T_(2) V_(f)^(gamma -1)`
` T_3 V_f^(r-1)-T_4 V_(f)^( gamma -1)`
Dividing Eq. 21-49 by Eq. 21-48, we get
`(T_4 )/( T_1) =(T_3)/(T_2)`
Subtracting 1 from both sides and solving, gives
`(T_4-T_1)/(T_1) =(T_3 -T_2)/(T_2)`
Rearranging above relation and using Eq. 21-48 gives
` (T_3 -T_1 )/(T_3-T_2) =(T_1)/(T_2) =((V_f))/(V_(i ))^( gamma -1)`
and therefore, the efficiency is
` epsi =1-((1)/(r))^( gamma -1)`
For `gamma` = 1.4 and r= 10, the efficiency is
`epsi =1- ( 0.10 )^(0.4 ) = 0.6 = 60 % `
The maximum possible efficiency, if the cycle would have been Carnot cycle, would be,` 1 - T_2//T_4`, as `T_2` and `T_4` are the lowest and highest temperatures in the cycle. It can be seen that efficiency is less than the Carnot efficiency as the value of `T_1 //T_2`, would be more than `Т_2 //T_4 `