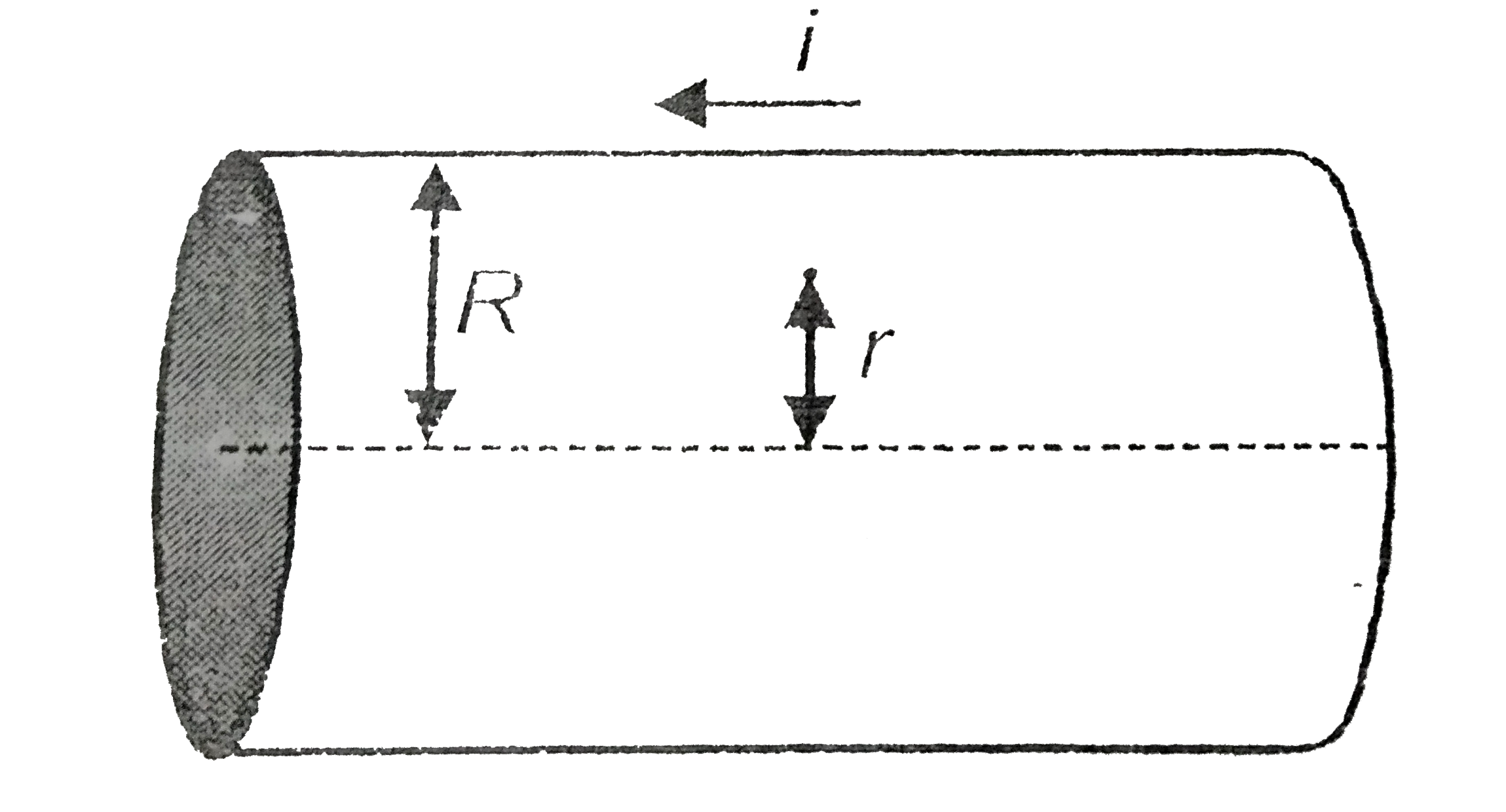
A long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as `J = kr^(2)`, where, k is a constant. Find an expression for the magnetic field B at a distance `r (lt R)` from the axis

A long cylidrical conductor of radius R carries a current i as shown in figure. The current desity J is a function of radius according to J=br , where b is a constant. Find an expression for the magnetic field B a. at a distasnce r_1ltR and b.at a distance r_2gtR, measured from the axis.

A long cylindrical conductor of radius R carries I as shown. The current density is a function of radius r as j = br, where b is a constant. The magnetic field at a distance r_(1)(r_(1)ltR) is

Consider an infinite long cylinderical conductor of radius R carrying a current I with a non uniform current density J=alphar where a is a constant. Find the magnetic field for inside and outside prints.

Suppose that the current density in a wife of radius a varies with r according to J = Kr^(2) , where K is a constant and r is the distance from the axis of the wire. Find the megnetic field at a point distance r from the axis when (a) r a

A non-homogeneous cylinder of radius "R" carries a current I whose current density varies with the radial "distance "r" from the centre of the rod as J=sigma r where sigma is a constant.The magnetic field at a point "P" at a distance r

A long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance r from the centre of the wire?

If the current density in a linear conductor of radius 'a' varies with r according to relation J=kr^2 , where k is a constant and r is the distance of a point from the axis of conductor. Find the magnetic field induction at a point distance r from the axis, when (i) rlta and (ii) rgta .

A long straight cylindrical region of radius a curries a current along its length. The current density (J) varies from the axis to the edge of the cylindrical region according to J = J_(0) ( 1 – r / a) Where r is distance from the axis (0 lt r lta) (a) Find the mean current density. (b) Plot the variation of magnetic field (B) with distance r from the axis of the cylinder for 0 lt r lt a .

A hollow cylindrical conductor of inner radius a and outer radius b carries a current I uniformly spread over its cross-section. Find the magnetic field induction at a point inside the body of the conductor at a distance r [where a lt r lt b ] from the axis of the cylinder.