Similar Questions
Explore conceptually related problems
Recommended Questions
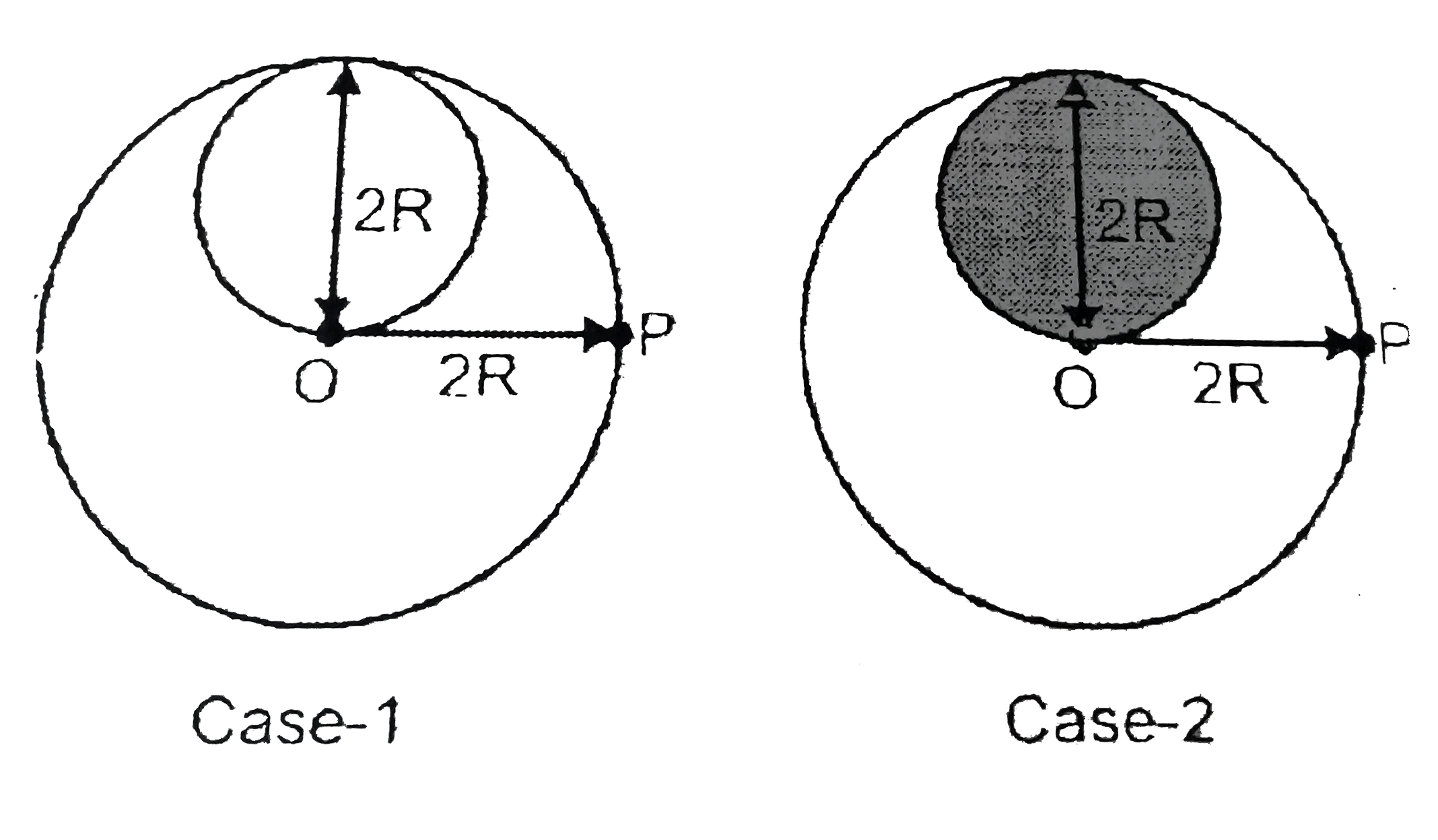
- A lamina is made by removing a small disc of diameter 2 R from a bigge...
Text Solution
|
- A lamina is made by removing a small disc of diameter 2R from a bigg...
Text Solution
|
- A circular disc of radius R is removed from a bigger circular disc of ...
Text Solution
|
- A small hole is made in a disc of mass M and radius R at a distance R/...
Text Solution
|
- A lamina is made by removing a small disc of diameter 2 R from a bigge...
Text Solution
|
- On the flat surface of a disc of radius a a small circular hole of rad...
Text Solution
|
- A circular disc of radius R is removed from a bigger circular disc of ...
Text Solution
|
- A circular disc of radius R is removed from a bigger circular disc of ...
Text Solution
|
- A circular disc of radius R is removed from a bigger circular disc of ...
Text Solution
|