Similar Questions
Explore conceptually related problems
Recommended Questions
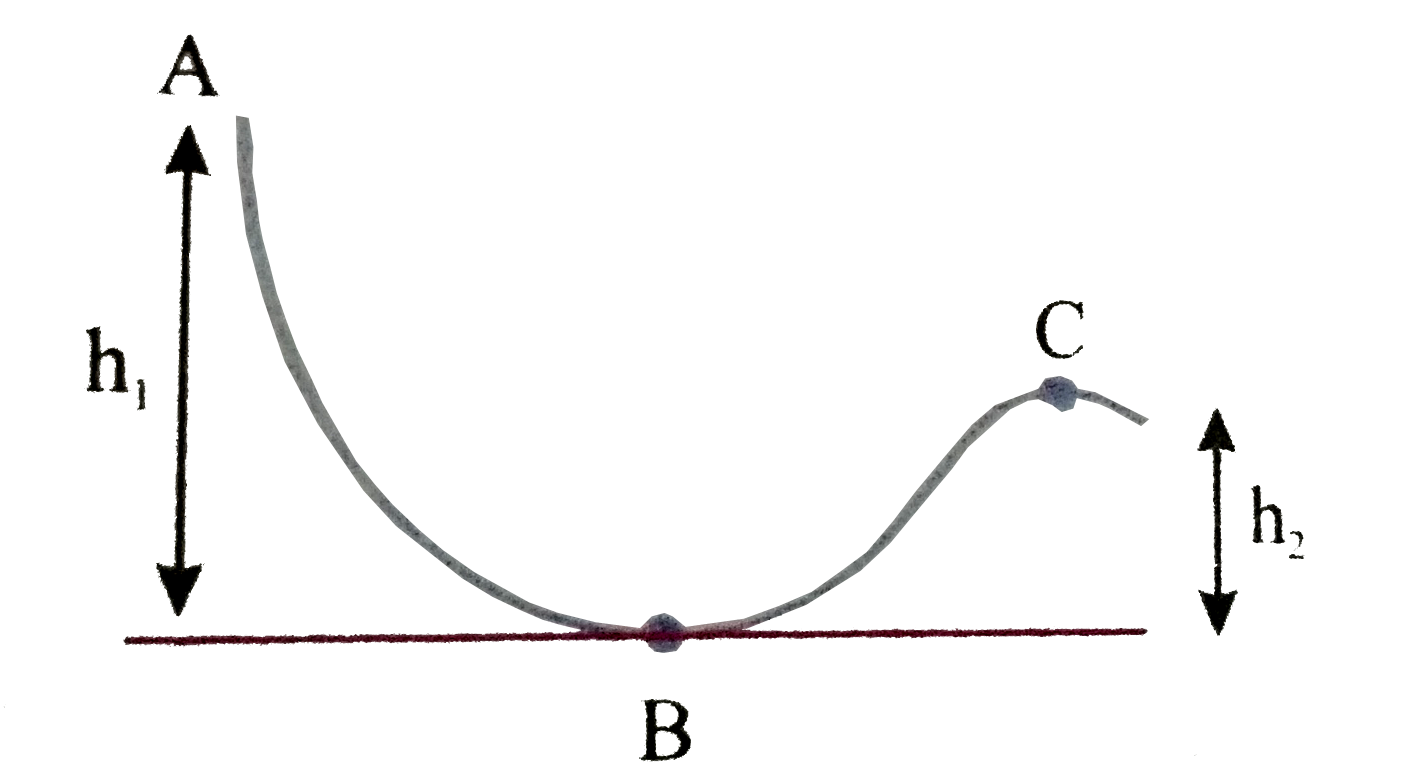
- A block of mass m = 1 kg is released from point A along a smooth track...
Text Solution
|
- The additional kinetic energy to be provided to a satellite of mass m ...
Text Solution
|
- A 400 kg satellite is in a circular orbit of radius 2 R(E) around the ...
Text Solution
|
- A block of mass m = 1 kg is released from point A along a smooth track...
Text Solution
|
- A block of mass m = 1 kg is released from point A along a smooth track...
Text Solution
|
- A block of mass m = 1 kg is released from point A along a smooth track...
Text Solution
|
- Three circles with radius r(1), r(2), r(3) touch one another externall...
Text Solution
|
- h(1) तथा r(1) क्रमश: एक शंकु जिसका छिन्नक एक भाग है, की ऊँचाई तथा त्रि...
Text Solution
|
- The height and radius of the cone of which the frustum is a part are h...
Text Solution
|
 .
.