Similar Questions
Explore conceptually related problems
Recommended Questions
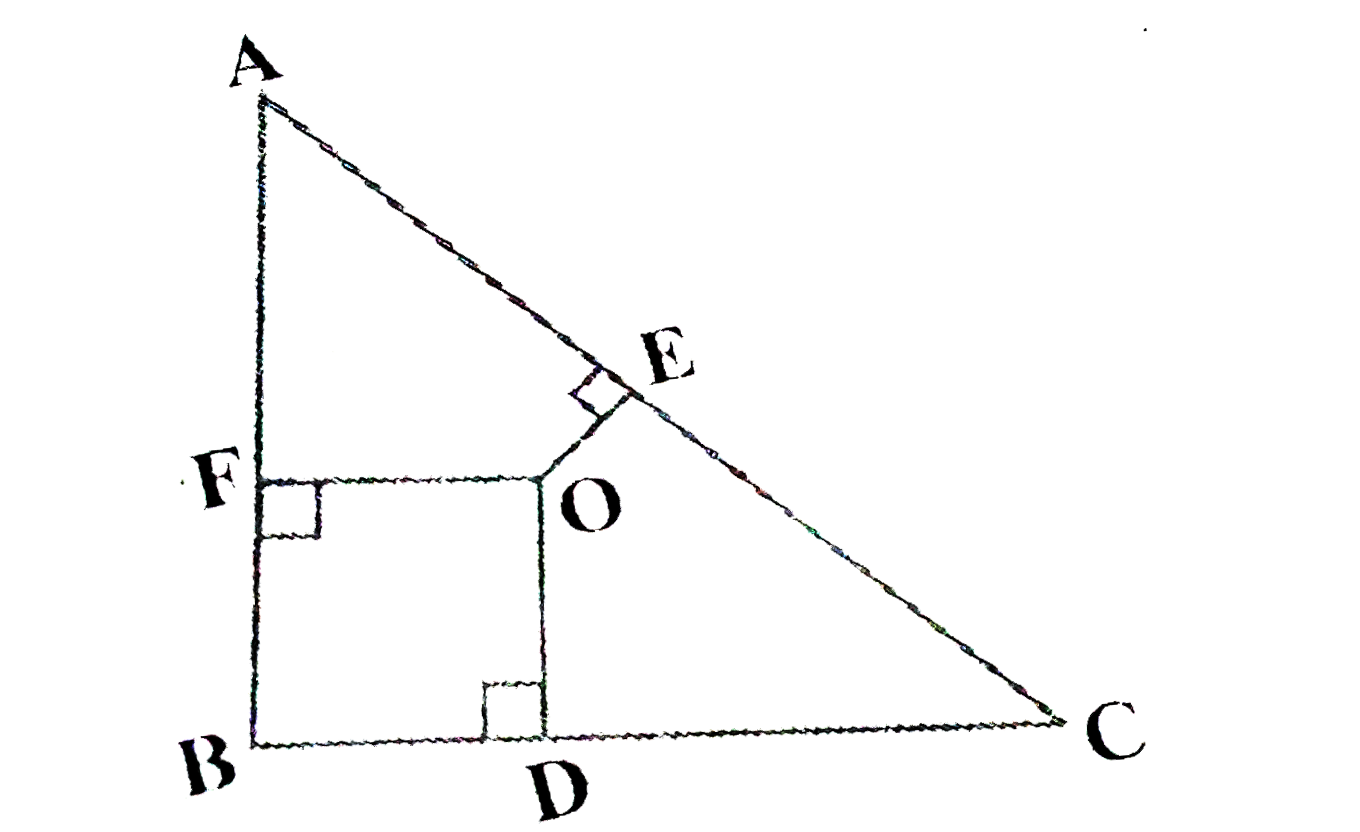
- In figure, O is a point in the interior of a triangle ABC, O D|B C ,O...
Text Solution
|
- In figure, O is a point in the interior of a triangle ABC, O D|B C ,O...
Text Solution
|
- A B C D IS A PARALLELOGRAM AND O is any point in its interior. Prov...
Text Solution
|
- If O\ a n d\ O^(prime) are circumcentre and orthocentre of \ A B C ,\ ...
Text Solution
|
- O is any point inside a rectangle ABCD. Prove that O B^2+O D^2=O A^2+...
Text Solution
|
- In figure, O is a point in the interior of a triangle ABC, O D|B C ,O...
Text Solution
|
- In A B C Prove that A B^2+A C^2=2(A O^2+B O^2) , where O is the ...
Text Solution
|
- O is any point inside a triangle A B C . The bisector of /A O B ,/B O ...
Text Solution
|
- From a point O in the interior of a A B C , perpendiculars O...
Text Solution
|