Similar Questions
Explore conceptually related problems
Recommended Questions
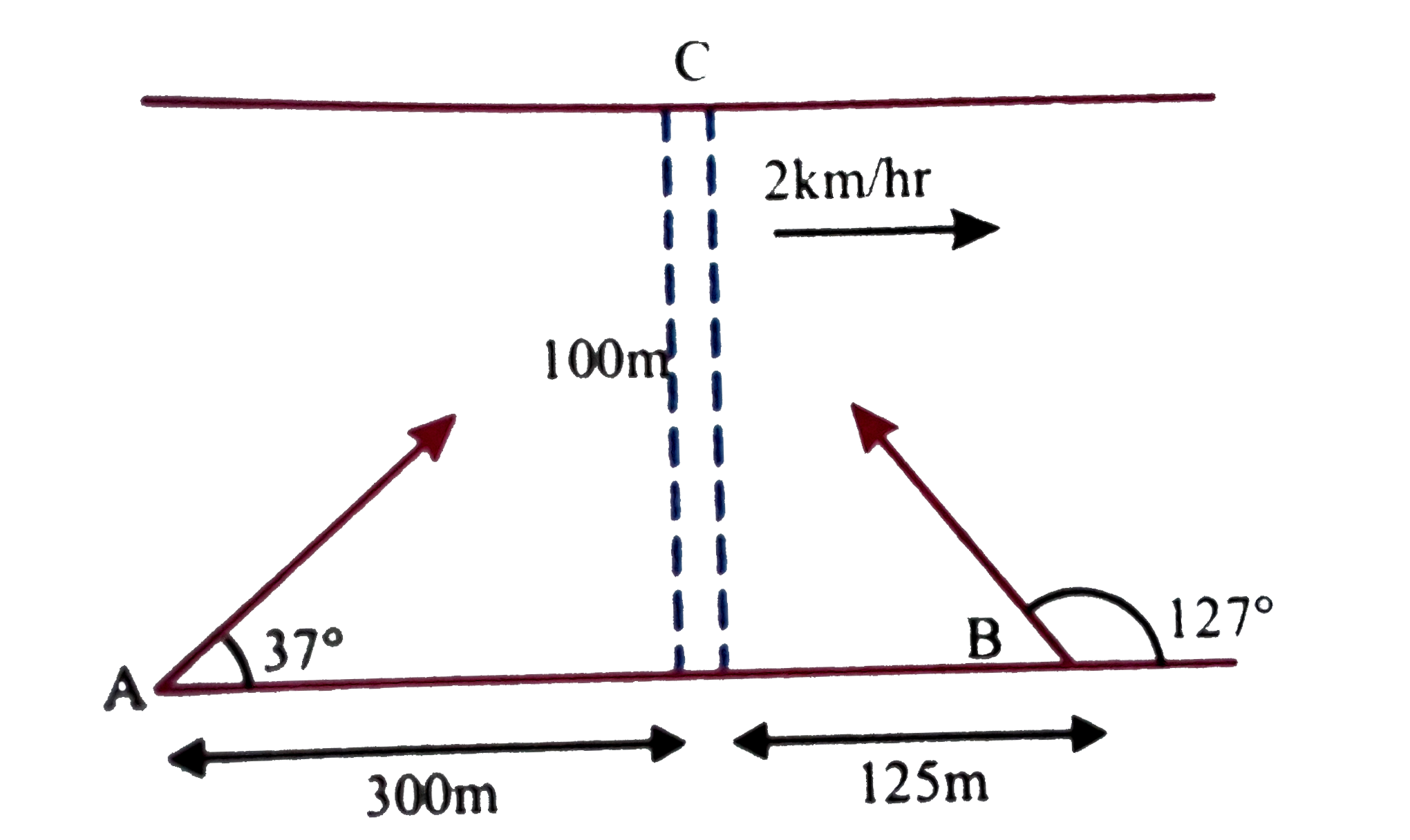
- Two swimmers start a race. One who reaches the point C first on the ot...
Text Solution
|
- A man who can swin at the rate of 2 (km)/hr) (in still river) crosses ...
Text Solution
|
- A swimmer swims in still water at a speed =5 km//hr . He enters a 200m...
Text Solution
|
- Two swimmers start a race. One who reaches the point C first on the ot...
Text Solution
|
- A swimmer wands to cross a river and reach point B directly from A. Th...
Text Solution
|
- A river is flowing with velocity 5km//hr as shown in the figure. A boa...
Text Solution
|
- A swimmer wishes to cross a 500m wide river flowing at a rate 5km/hr. ...
Text Solution
|
- A river is flowing with a speed of 1 km/hr. A swimmer wants to go to p...
Text Solution
|
- एक नदी में पानी 1.5nkm//h के वेग से बह रहा है । एक तैराक शांत जल में 4...
Text Solution
|