Similar Questions
Explore conceptually related problems
Recommended Questions
- All surfaces assumed to be frictionless calculate the horizontal force...
Text Solution
|
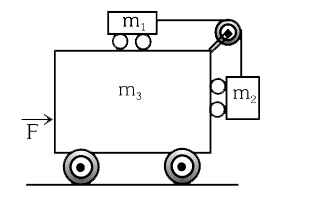
- In the adjoining figure all surface are frictionless . What force F mu...
Text Solution
|
- For the system shown in fig, there is no friction anywhere. Masses m(1...
Text Solution
|
- Three block of masses m(1),m(2) and m(3) kg are placed in contact with...
Text Solution
|
- In the figure2.217 all the surfaces are frictionless. What force F is ...
Text Solution
|
- A horizontal force F is applied on a riing of mass m(1) constrained to...
Text Solution
|
- What force F must be applied so that m(1) and m(2) are at rest on m(3)...
Text Solution
|
- When force F applied on m(1) and there is no friction between m(1) and...
Text Solution
|
- When force F applied on m(1) and surface. Is mu(1) and the coefficient...
Text Solution
|