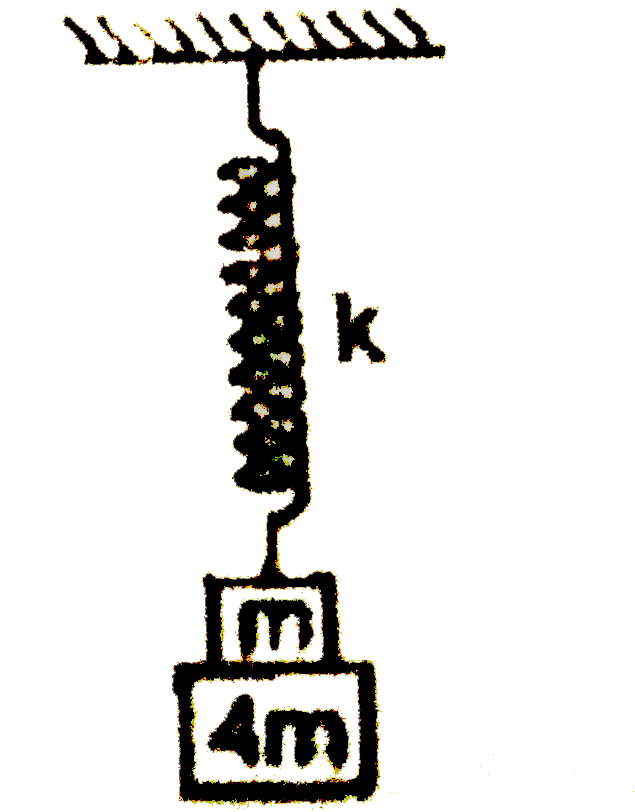Similar Questions
Explore conceptually related problems
Recommended Questions
- Find how much m will rise if 4m falls away. Block are at rest and in e...
Text Solution
|
- Find how much mass m will rise if 4m falls away. Blocks are at rest an...
Text Solution
|
- A 16kg block moving on a frictionless horizontal surface with a veloci...
Text Solution
|
- In the arrangement shown in the figure the system is in equilibrium. M...
Text Solution
|
- A block of mass M is tied to a spring of force constant K and the syst...
Text Solution
|
- Find how much m will rise if 4m falls away. Block are at rest and in e...
Text Solution
|
- Equilibrium price falls and equilibrium quantity rises when:
Text Solution
|
- The block of mass m is at rest. Find the tension in the string A .
Text Solution
|
- A projectile rises to a height of 10 m and then falls at a distance of...
Text Solution
|