Home
Class 11
PHYSICS
Two stones are thrown up simultaneously ...

Two stones are thrown up simultaneously from the edge of a cliff ` 200 m` high with initial speeds of ` 15 ms^(-1)` and ` 30 ms^(-1)`. Verify that the graph shown in Fig. 2 ( NCT). 13 , correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect the air resistance and assume that the stones do not rebound after hitting the ground. Take ` g= 10 ms^(-2)`.Give equations for the linear and curved parts of the plot.
.

Text Solution

Verified by Experts

Consider the upwared motion of 1st stone:
`x_(0)=200m, u=15ms^(-1),g=-10ms^(-2),x=x`
`x_(1)=x_(0)+ut+(1)/(2)gt^(2)`
`x_(1)=200+15t-5t^(2)`
When first stone hits the ground then
`x_(1)=0`, we get `200+15t-5t^(2)=0`
`t^(2)-3t-40=0`
solving we get `t=-5s` or t=8s
As t=-5 s is meaningless
Therefore t=8s
Similarly when `2^("nd")` stone hits the ground then
`x_(2)=0`
`x_(0)=200m,u=30ms^(-1),g=-10ms^(-2),x=x_(2)`
We get `x_(2)=x_(0)+ut+(1)/(2)gt^(2)`
`0=200+30t-5t^(2)`
`200+30t-5t^(2)=0`
or `t^(2)-6t-40=0`
Solving we get `t=-4`, or t=10s
As t=-4 is meaningless
therefore, t=10s.
From i and ii we get relatie position of second stone w.r.t. first stone
`x_(2)-x_(1)=15t`
The first stone will be in motion for 8 seconds
As `x_(2)-x_(1)=t`
Therefore graph will be a straight line for t=8 sec. and the maximum separation between two stones
`=15t=15xx8=120m`
After 8sec, only `2^("nd")` stone will be in motion and the graph is in accordance with the equation `x_(2)=200+30t-15t^(2)` for an interval between 8s. to 10s.
Promotional Banner

Topper's Solved these Questions

  • MOTION IN A STRAIGHT LINE

    MODERN PUBLICATION|Exercise NCERT (VERY SHORT ANSWER TYPE QUESTION)|5 Videos

  • MOTION IN A STRAIGHT LINE

    MODERN PUBLICATION|Exercise NCERT (SHORT ANSWER TYPE QUESTION)|6 Videos

  • MOTION IN A STRAIGHT LINE

    MODERN PUBLICATION|Exercise NCERT (TEXTBOOK EXERCISES )|22 Videos

  • MOTION IN A PLANE

    MODERN PUBLICATION|Exercise Chapter Practice Test|15 Videos

  • OSCILLATIONS

    MODERN PUBLICATION|Exercise Practice Test (For Board Examination)|12 Videos

Similar Questions

Explore conceptually related problems

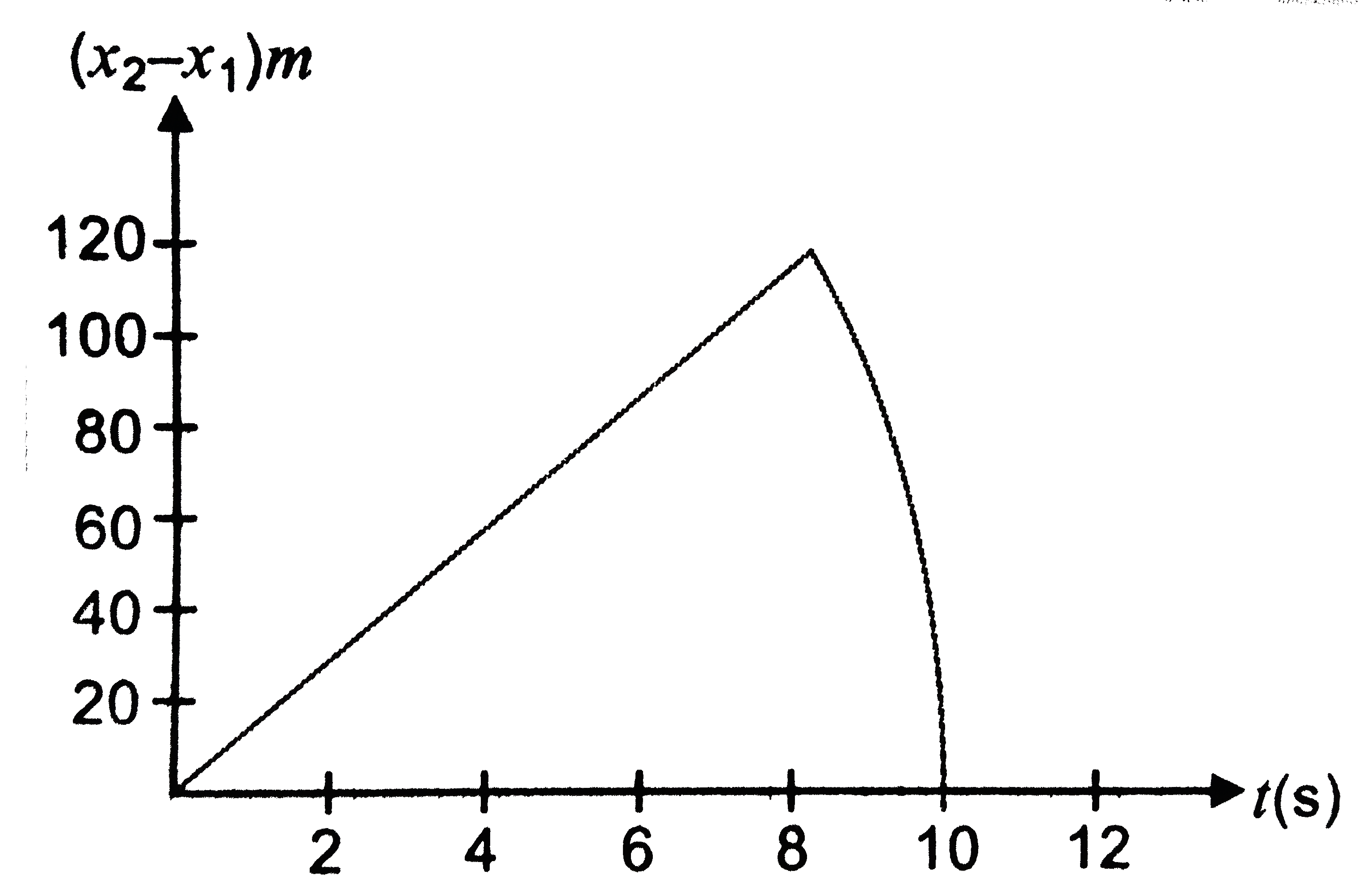
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 ms?^(-1) and 30^(-1) . Verify that the graph shown in Fig. 2 ( NCT). 13 , correctly represents the time variation of the relativ e position of the second stone with respect to the first. Neglect the air resistance and assume that the stones do not rebound after hitting the ground. Taje g= 10 ms^(-2) .Give equations for the linear and curved parts of the plot. .

Two stones are thrown up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m//s and 40 m//s respectively . Which of the following graph best represents the time variation of relative position of the speed stone with respect to the first ? ( Assume stones do not rebound after hitting the groumd and neglect air resistance , take g = 10 m//s^(2)) ( The figure are schematic and not drawn to scale )

Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g= 10 m//s^(2) (The figures are schematic and not drawn to scale)

Two stones are thrown up simultaneously with initial speeds of u_(1) and u_(2)(u_(2)gt_(1) u_(1)) . They hit the ground after 6 s and 10 s respectively. Which graph in fig. correctly represents the time variation of Deltax=(x_(2)-x_(1)) the relative position of the second stone with respect to the first upto t=10 s? Assume that the stones do not rebound after hitting the ground.

Two stones are thrown up simultaneously from the edge of a cliff with initial speed v and 2 v . The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.

A stone is thrown upwards and it rises to a height 0f 200m. The relative velocity of the stone with respect to the earth will be maximum at :-

Two stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed u_(1) = 30 m//sec and u_(2) = 50 m//sec . Which of the curve represent correct variation (for the time interval in which both reach the ground) of (x_(2) - x_(1)) = the relative position of second stone with respect to first with time (t) (v_(2) - v_(1)) = the relative velocity of second stone with respect to first with time (t). Assuming that stones do not rebound after hitting.