Similar Questions
Explore conceptually related problems
Recommended Questions
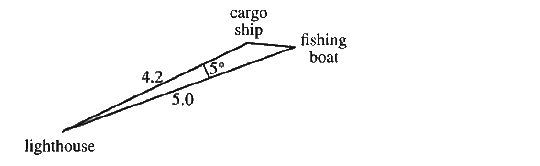
- A cargo ship is 4.2 miles from a lighthouse, and a fishing boat is 5.0...
Text Solution
|
- From the top of a lighthouse 120m above the sea, the angle of depressi...
Text Solution
|
- From the top of a lighthouse, 100 m high, the angle of depression of ...
Text Solution
|
- From a top of a lighthouse, an observer looks at the ship and find the...
Text Solution
|
- The angle of depression of a ship as observed from the top of a lighth...
Text Solution
|
- From the top of a lighthouse , an observer looks at a ship and finds t...
Text Solution
|
- The angles of elevation of the top of a lighthouse from 3 boats A,B an...
Text Solution
|
- A cargo ship is 4.2 miles from a lighthouse, and a fishing boat is 5.0...
Text Solution
|
- Two ships are sailling in the sea on the two sides of a lighthouse. If...
Text Solution
|