We can find the magnetic field `vecB` at point C by applying the Biot-Savart law of Eq. 29-3 to the wire, point by point along the full length of the wire. However, the application of Eq. 29-3 can be simplified by evaluating `vecB` separately for the three distinguishable sections of the wire namely (1) the straight section at the left (2) the straight section at the right, and (3) the circular arc.
Straight sections : For any current-length element in section1, the angle `theta` between `dvecs` and `hatr` is zero (Fig. 29-14b) , so Eq. 29-1 gives as
`dB_(1)=(mu_(0))/(4pi)(ids sintheta)/(r^(2))=(mu_(0))/(4pi)(idssintheta)/(r^(2))=0`
Thus, the current along the entire length of straight section 1 contributes no magnetic field at C
`B_(1)=0`
The same situation prevails in straight section 2, where the angle `theta` between `dvecs` and `hatr` for any current length element is `180^(@)`. Thus,
`B_(2)=0`
Circular arc : Application of the Biot-Savart law to evaluate the magnetic field at the center of a circular arc leads to Eq. 29-9 `(B=mu_(0)iphi//4piR)`. Here the central angle `phi` of the arc is `pi//2` rad . Thus from Eq. 29-9, the magnitude of the magnetic field `vecB_(3)` at the arc .s center C is
`B_(3)=(mu_(0)i(pi//2))/(4piR)=(mu_(0)i)/(8R)`
To find the direction of `vecB_(3)`, we apply the right-hand rule displayed in Fig. 29-5. Mentally grasp the circular arc with your right hand as in Fig. 29-14c, with your thumb in the direction of the current. The direction in which your fingers curl around the wire indicates the direction of the magnetic field lines around the wire. They form circles around the wire, coming out of the page above the arc and going into the page inside the arc. In the region
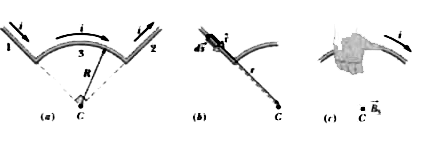
of point C (inside the arc), your fingertips point into the plane of the page. Thus , `vecB_(3)` is directed into that plane.
Net field : Generally we combine multiple magnetic fields as vectors. Here, however, only the circular arc produces a magnetic field at point C. Thus , we can write the magnitude of the net field `vecB` as
`B=B_(1)+B_(2)+B_(3)=0+0+(mu_(0)i)/(8R)=(mu_(0)i)/(8R)`
The direction of `vecB` is the direction of `vecB_(3)` namely into the plabe of Fig 29-14

