Home
Class 12
PHYSICS
If a fish lies at the bottom of a 4 m d...

If a fish lies at the bottom of a 4 m deep water tank `(mu = 4//3)` and a bird is flying at a height of 6m above the water surface, then apparent distance at which the fish appears to the bird is

Text Solution

Verified by Experts

Notice that the boy is viewing the fish normally. The rays emanating from fish do not directly reach the boy, they undergo refraction at the water air interface. It seems that the rays should not deviate at all when we are viewing normally. However, it is not one single ray that we are going to use for the formation of image. There is a narrow pencil of rays which refract to form an image. So, we can use the formula for the apparent depth (Eq. 34-3) that we derived just before.
Calculation : Given that the rays are incident from water to air. So `n_(i)` is 4/3 and `n_(r )` is 1. The depth is measured from the water surface, so the depth is taken to be `h//2`. Now,
`(d_(1))/(mu_(r ))=(d_(0))/(mu_(i))`
`(d_(app))/(1)=((h)/(2))/((4)/(3))`.
As discussed before, this answer is the distance from the water surface .
Distance from the observer is
`(3h)/(8)+h=(11h)/(8)`.
(b) Find the apparent distance at which the boy sees the image of the fish (reflected in the mirror at the bottom).

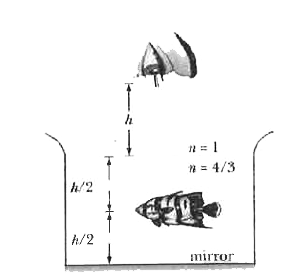
(1) Here, we can see that first rays from fish are reflected from the mirror. These reflected rays will again strike the water surface and after refraction from there, final image will be formed. Here two events occur one after another.
(2) Reflection from the mirror : For this, the object is at a distance h/2 from the mirror. So, the image will be formed at a distance h/2 behind the mirror. Note that although this image will be formed behind the mirror, no refraction will occur to form this image. Therefore, we need not consider the apparent depth while considering this reflection. This image will act as an object for refraction from water surface. For this refraction, the distance is measured from the water surface.
Calculation : The distance of this object from the water surface will be `h+(h//2)=3h//2`. Therefore,
`(d_(app))/(1)=((3h)/(2))/((4)/(3))=(9h)/(8)`.
So, distance from observer is
`(9h)/(8)+h=(17h)/(8)`
Although the object here is in air (image behind the mirror), we need not consider the refractive index of air because in the formula for the apparent depth, we consider the refractive index for the incident rays and that for the refracted rays.
Note : If you are still having a doubt as to what refers to `n_(i)` and what refers to `n_(r )`, draw a ray diagram to see the formation of image.
Promotional Banner

Topper's Solved these Questions

  • GEOMETRICAL OPTICS : REFRACTION

    RESNICK AND HALLIDAY|Exercise Check point|6 Videos

  • GEOMETRICAL OPTICS : REFRACTION

    RESNICK AND HALLIDAY|Exercise Problems|44 Videos

  • GEOMETRICAL OPTICS : REFLECTION

    RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (Integer Type)|3 Videos

  • GRAVITATION

    RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (INTEGER TYPE)|4 Videos

Similar Questions

Explore conceptually related problems

A fish lies at the bottom of a 4 m deep water lake. A bird flies 6m above the water surface and refractive index of water is 4//3 . Then the distance between

A concave mirror with its optic axis vertical and mirror facinig upward is placed at the bottom of the water tank. The radius of curvature of the mirror is 40 cm and refractive index for water mu=4//3 . The tank is 20 cm deep and if a bird is flying over the tank at a height of 60 cm above the surface of water, find the position of image of the bird.

A bird is flying 3m above the surface of water. To a fish underwater, the height of the bird from the water surface appears to be

A plane mirror is fixed at the bottom of a vessel as shown in the figure. Water of refractive index mu is filled up to a height h in the vessel. There is a fish at a height h//2 from bottom of vessel and there is a bird at a height h above the surface of water in the vessel. (a) Calculate apparent distance of bird as seen by the fish. (b) Calculate apparent distance of image of bird in mirror as seen by the fish. (c) Calculate apparent distance of fish as seen by the bird. (d) Calculate apparent distance of image of fish in the mirror as seen by the bird.

An under water swimmer is at a depth of 12 m below the surface of water. A bird is at a height of 18 m from the surface of water, directly above his eyes. For the swimmer the bird appears to be at a distance from the surface of water equal to (Refractive Index of water is 4/3)

Two holes are made in the side of the tank such that the jets of water flowing out of them meet at the same point on the ground. If one hole is at a height of 3 cm above the bottom, then the distance of the other holes from the top surface of water is

A 2 cm diameter coin rests flat on the bottom of a bowl in which the water is 20 cm deep (mu_(w) = 4//3) . If the coin is viewed directly from above, what is its apparent diameter ?

A man looks down on a fish of length 20 cm. His eye is 2m above the surface of the water (mu = 4//3) and the fish is 2m below the surface as shown in the figure the ratio of angular width Delta theta of the fish as seen by the man in presence of water to the Delta theta in the absence of water is (Delta theta is small)