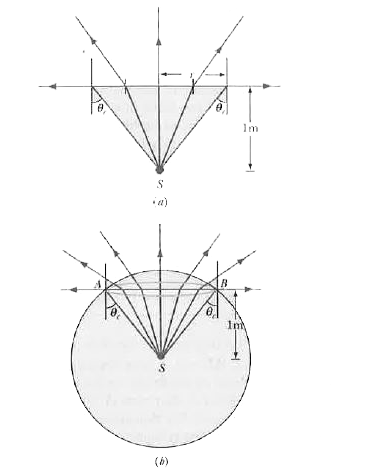
Just vertically above the point source, the angle of incidence is `0^(@)`. As we move sideways, the angle of incidence will increase. So, the angle of refraction will also increase. Since the rays are going from denser to the rarer medium, the rays will bend away from the normal. At the position where the angle of refraction becomes `90^(@)`, the angle of incidence will be critical angle. A little visualization says that this condition will be achieved at all the points on a circle just above the source.
Calculation : Form Eq. 34-10 `[theta_(c )=sin^(-1)(n_(1)//n_(2))]`, we get
`1.25sintheta_(c )=1 sin 90^(@)`
Therefore,
`theta_(c )=53^(@)`
From the triangle made by the radius of the circle and the vertical line, we can say that
`tantheta=(r )/(1)`
or `r=1tantheta=(4)/(3)`
(b) If the power of source is P find the power coming out of surface `(n_("water")=4//3)`.
(1) Here, we are required to find the part of the power which is incident on the circular patch whose radius we found just now. An associated concept here is the concept of intensity. If a source of power P is kept at a certain point, the light energy emitted by it will be transmitted equally in all the directions . So, we can say that after some time, this light energy will be distributed on the surface of a sphere of radius R=ct.
Intensity at that point is defined as
`("Power")/("Area over which light is distributed ")=(P)/(4piR^(2))`
where R is the distance from source at which we are measuring the intensity.
(2) It is clear here that if a disk is kept in the path of the light rays (this disk may be a mirror, a slab etc), a part of the light energy will be incident on the disk. If we wish to find the amount of light energy incident on the disk, we should note that disk is obstructing that part of the light energy which would have been distributed on the part of the sphere denoted by AB (see fig. 34-20b).
Here we can see that since the light energy is equally distributed on all parts of the sphere, the amount of light energy incident on the disk is proportional to area A of the spherical portion above the water surface :
`(P_(s))/(P)=(A)/(4piR^(2))`
(3) Recall the concept of solid angle discussed in Chapter 23. There we showed how solid angle .
`Omega=(A)/(R^(2))=2pi(1-costheta)`
To find the power passing through this circular patch, we should find the power emitted by the source in the cone of half angle `theta_(c )=53^(@)`
From the concept discussed above, the contained in this cone is in proportion of solid angle subtended by the cone at the source. Therefore,
`Omega` (solid angle) `=2pi(1-costheta)=(A)/(r^(2))`
The solid angle is measured in steredians. Now,
`P_(S)=Pxx(Omega)/(4pi)`
`=(P)/(4pi)2pi(1-costheta)=(3P)/(10)`
Note : The actual power will be somewhat less than this value because we have neglected the partial reflection at the water surface.