Similar Questions
Explore conceptually related problems
Recommended Questions
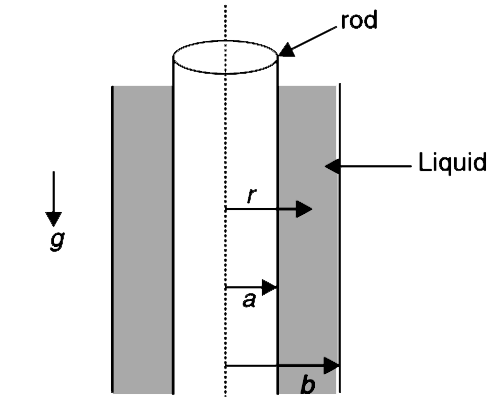
- A vertical steel rod has radius a. The rod has a coat of a liquid film...
Text Solution
|
- In dimension of circal velocity v(0) liquid following through a take a...
Text Solution
|
- A container filled with viscous liquid is moving vertically downwards ...
Text Solution
|
- What is the velocity v of a metallic ball of radius r falling in a tan...
Text Solution
|
- A vertical steel rod has radius a. The rod has a coat of a liquid film...
Text Solution
|
- A sphere of radius R is gently dropped into liquid of viscosity eta in...
Text Solution
|
- If dimensions of critical velocity of a liquid vc flowing through a tu...
Text Solution
|
- A small spherical body of radius r made of material of density rho is ...
Text Solution
|
- A certain number of spherical drops of a liquid of a liquid of radius ...
Text Solution
|