Similar Questions
Explore conceptually related problems
Recommended Questions
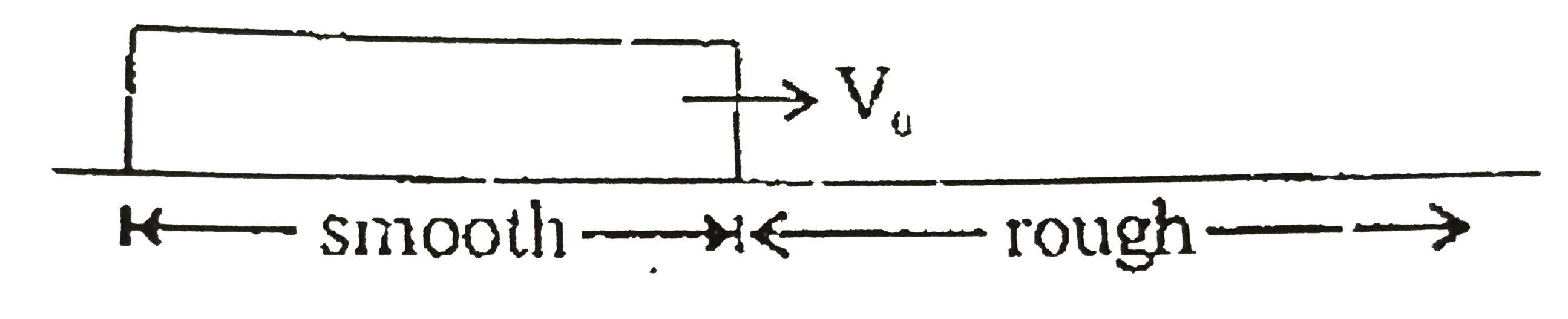
- A uniform rod of length 1m lies on the smooth part of a horizontal sur...
Text Solution
|
- A uniform rod of mass M and length L, area of cross section A is place...
Text Solution
|
- A thin uniform rigid rod of mass m and length l is in mechanical equil...
Text Solution
|
- A uniform rod of length l is kept vertically on a rough horizontal sur...
Text Solution
|
- A uniform metallic rod lies on a smooth horizontal surface. C is centr...
Text Solution
|
- A uniform rod of length 1m lies on the smooth part of a horizontal sur...
Text Solution
|
- खुरदरे (रुक्ष) क्षैतिज पृष्ठ पर रखे 20 किग्रा द्रव्यमान के गुटके को ठी...
Text Solution
|
- A block slides with a velocity of 10 m/s on a rough horizontal surface...
Text Solution
|
- A uniform rod ABC of mass M is placed vertically on a rough horizontal...
Text Solution
|