Similar Questions
Explore conceptually related problems
Recommended Questions
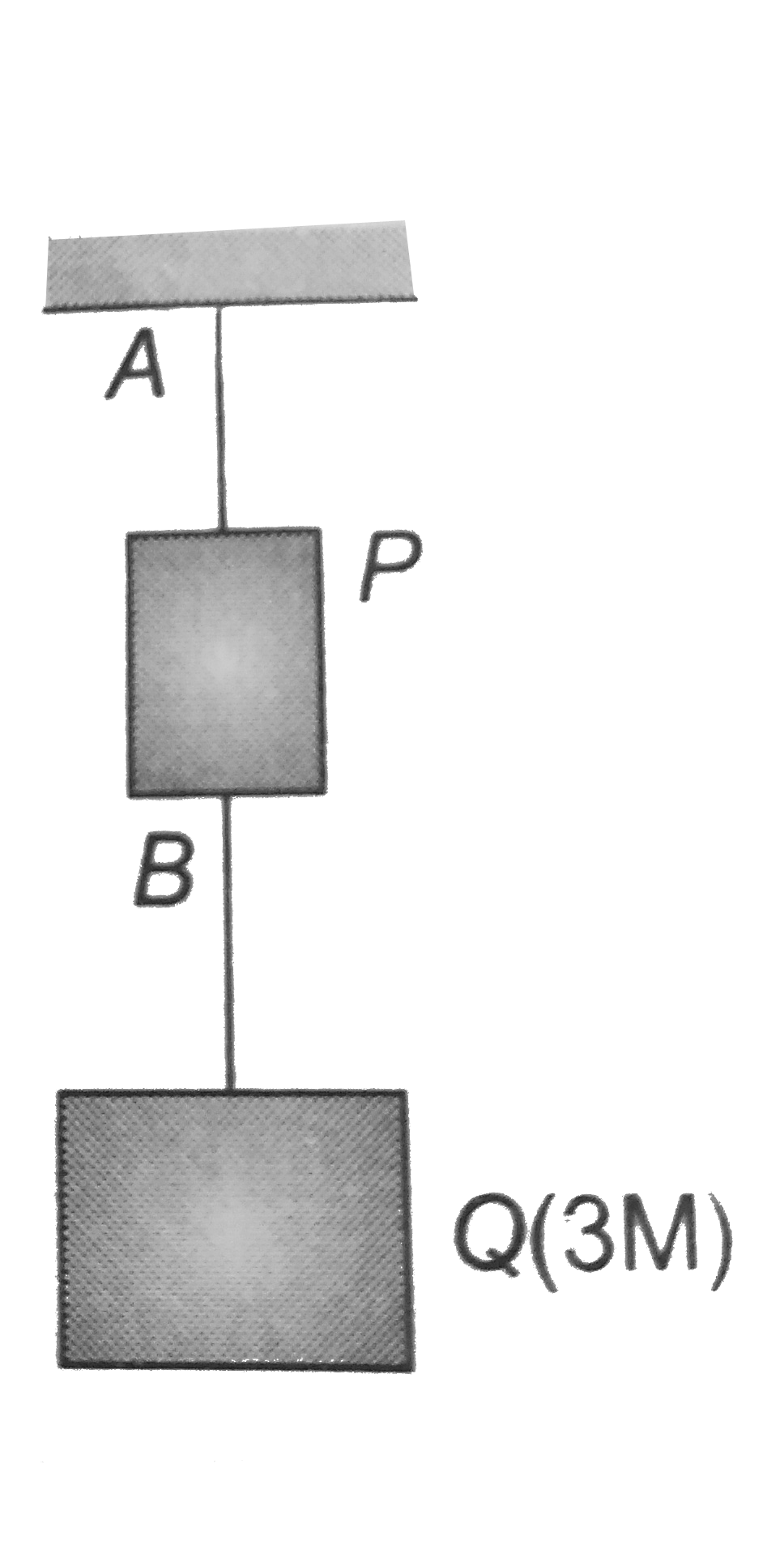
- Wires A and B are connected with blocks P and Q, as shown, the ratio o...
Text Solution
|
- If the ratio of lengths, radii and Young's moduli of steel and brass w...
Text Solution
|
- Wires A and B are connected with blocks P and Q, as shown, the ratio o...
Text Solution
|
- 1 meter long metallic wire is broken into two unequal parts P and Q P ...
Text Solution
|
- If the ratio of lengths, radii and Young's moduli of steel and brass w...
Text Solution
|
- One metre long metallic wire is broken into two unequal parts P and Q....
Text Solution
|
- If the ratio of diameters,lengths and Young's moduli of steel and bras...
Text Solution
|
- If the ratio of lengths, radii and young's modulii of steel and brass ...
Text Solution
|
- A 2m long metallic wire is broken into two unequal points P and Q. P p...
Text Solution
|