Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RS AGGARWAL-MEASUREMENT OF ANGLES-Exercise 14
- If the arcs of the same length in two circles subtend angles of 60^(@)...
Text Solution
|
- Using a protractor, draw each of the following angles. (i) 60^(@), (...
Text Solution
|
- Express each of the following angles in radians. (i) 36^(@) , (ii) 1...
Text Solution
|
- Express each of the following angles in degrees. (i) ((5pi)/12)^(c )...
Text Solution
|
- The angles of a triangle are in AP and the greatest is double the leas...
Text Solution
|
- The difference between the two acute angles of a right triangleis (pi/...
Text Solution
|
- Find the radius of a circlein which a central angle of 45^(@) intercep...
Text Solution
|
- The length of an arc of a radius of 14 cm which subtends an angle of 3...
Text Solution
|
- If the arc of the same length in two circles subtend angles 75^(@) and...
Text Solution
|
- Find tge degree measure of the angle subtended at the centre of a circ...
Text Solution
|
- In a circle of diameter 30 cm, the length of a chord is 15 cm. Find th...
Text Solution
|
- The measure of angle in degrees through which a pendulum swings if its...
Text Solution
|
- The large hand of a clock is 42 cm long. How many centimetres does its...
Text Solution
|
- A wheel makes 180 revoluations in 1 minutes. Through how many radians ...
Text Solution
|
- A railway train is travelling on a circular curve of 1500 metres radiu...
Text Solution
|
- A wire of length 121 cm is bent so as to lie along the arc of a circle...
Text Solution
|
- The angles of a quadrilateral are in AP, and the greatest angle is dou...
Text Solution
|
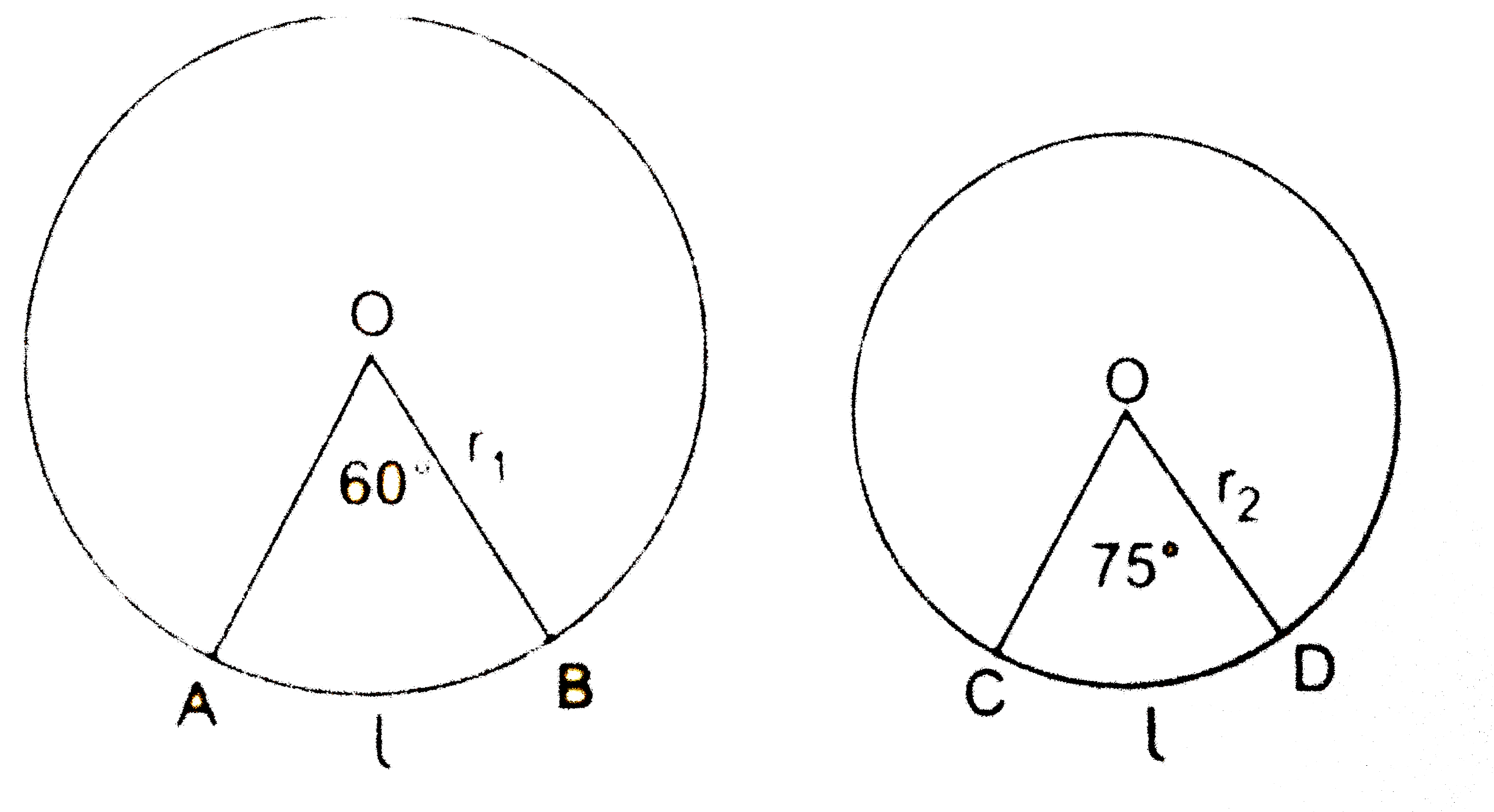 .
.