Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
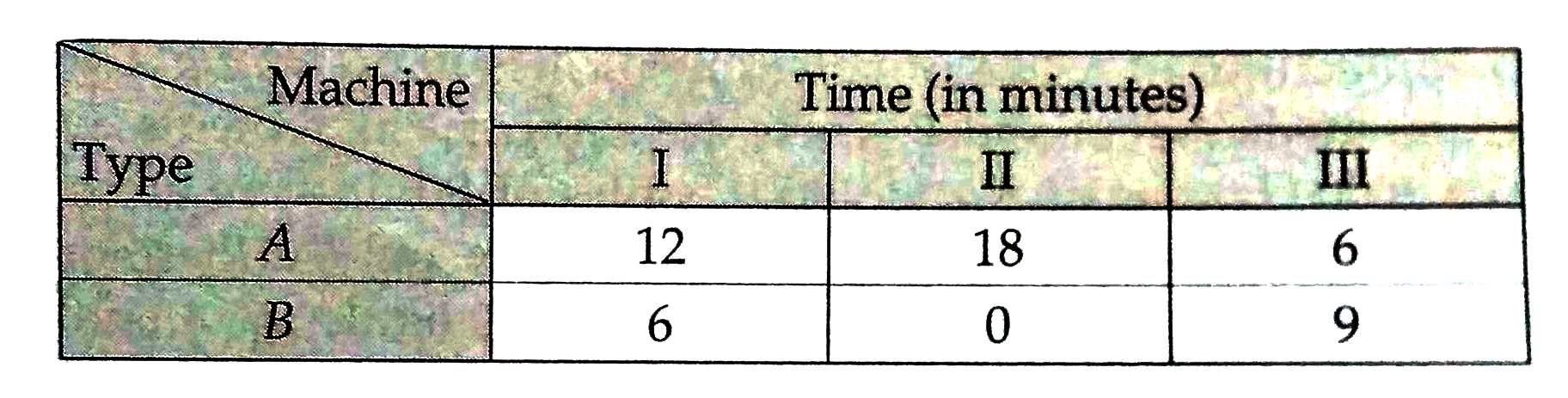
- A manufacturer makes two types, A and B of teapots. Three machines are...
Text Solution
|
- A manufacturer makes two types of toys A and B. Three machines are ne...
Text Solution
|
- A manufacturer makes two types of toys A and B. Three machines are ne...
Text Solution
|
- The inequation represented by the graph given below is : <img src="htt...
Text Solution
|
- The inequation that best describes the graph given below is <img src=...
Text Solution
|
- A manufacture makes two types of cups A and B. Three machines are requ...
Text Solution
|
- A manufacturer makes two types of toys A and B. Three machines are nee...
Text Solution
|
- A manufacturer makes two type of toys A and B. Three machines are need...
Text Solution
|
- A manufacturer maks two types A and B of tea cups. Three machines are ...
Text Solution
|