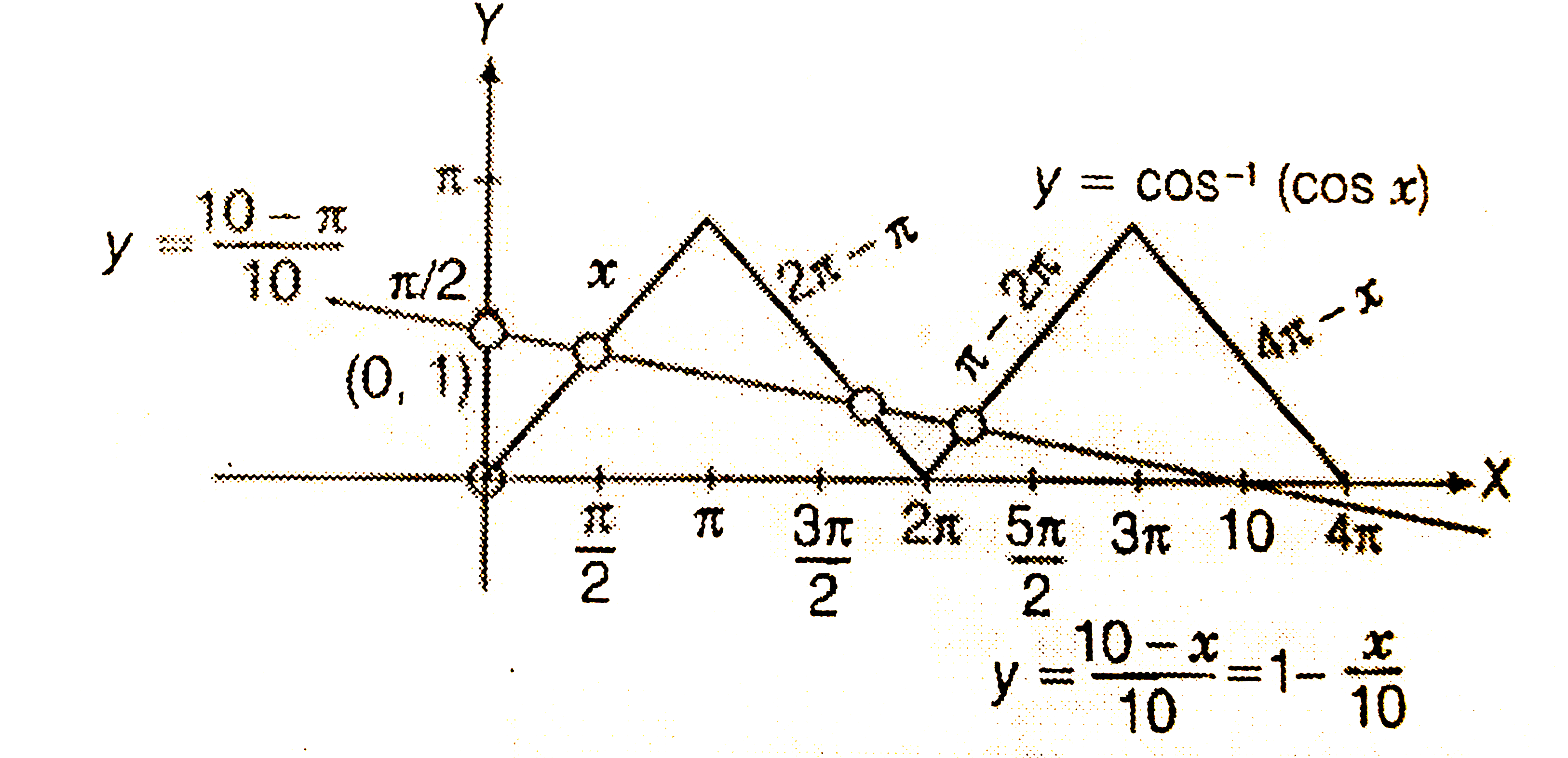Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let f:[0,4pi]->[0,pi] be defined by f(x)=cos^-1(cos x). The number ...
Text Solution
|
- Let f:[0,4 pi]rarr[0,pi] be defined by f(x)=cos^(-1)(cos x). The numbe...
Text Solution
|
- Let f(x)=sec^(-1)(x-10)+cos^(-1)(10-x) Then range of f(x) is
Text Solution
|
- Let the function f(x) = tan^(1-) (sin x + cos x) be defined on [ 0, 2 ...
Text Solution
|
- The number of points of discontinuity for f(x) sgn=(sin x), x in [0,4...
Text Solution
|
- Let, f:[0,4pi]to[0,pi] be defined by f(x)=cos^(-1)(cosx). The number o...
Text Solution
|
- Let f:[0,4 pi]rarr[0,pi] be defined by f(x)=cos^(-1)(cos x) then numbe...
Text Solution
|
- माना f: [0,4pi] to [0,pi], f(x)=cos^(-1)(cosx) के द्वारा परिभाषित है। ...
Text Solution
|
- Let f:[0,4pi]->[0,pi] be defined by f(x)=cos^-1(cos x). The number ...
Text Solution
|