A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
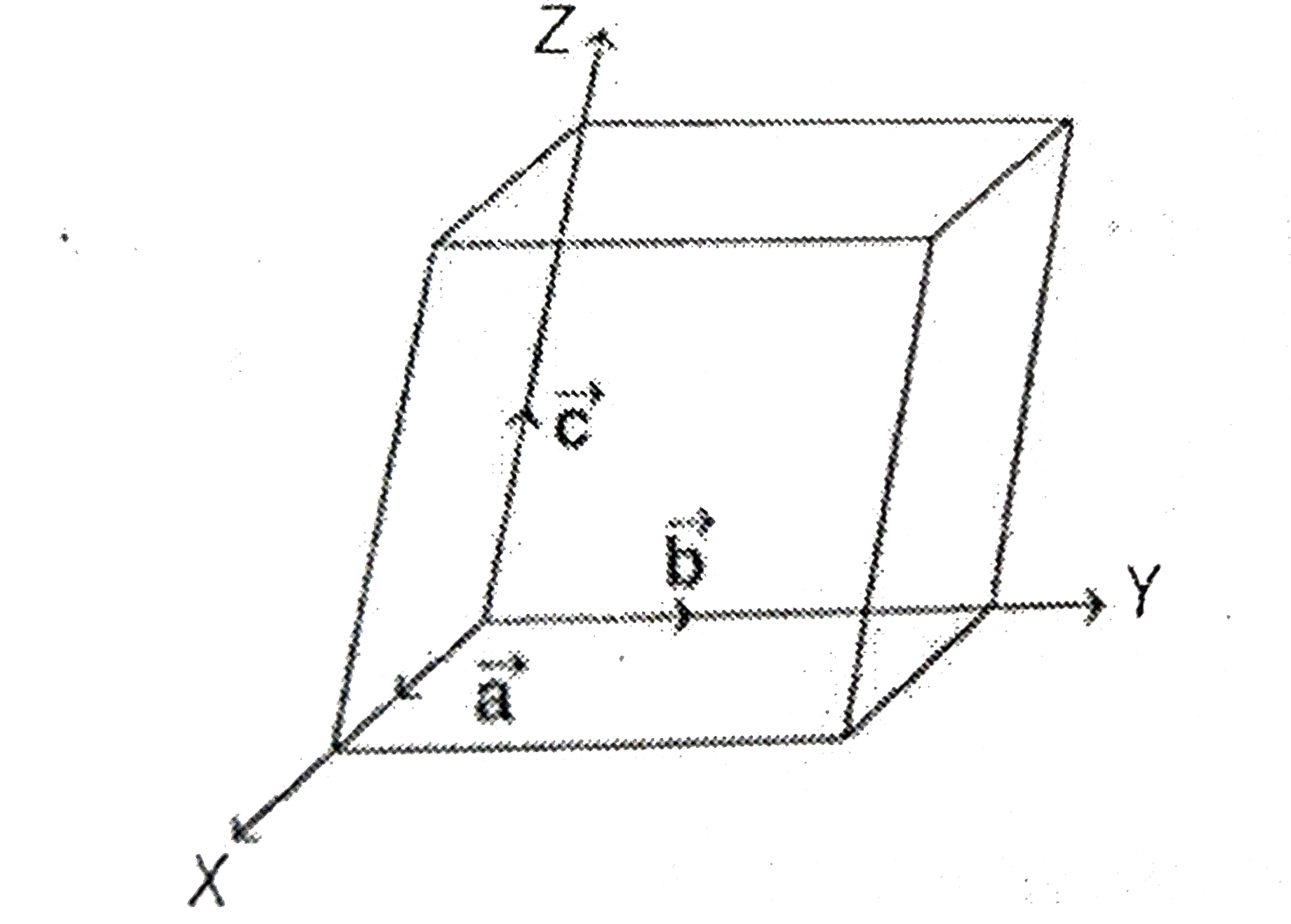
- The deges of a parallelopied are of unit length and are parallel ...
Text Solution
|
- The edges of a parallelopiped of unit length are parallal to non-copla...
Text Solution
|
- The deges of a parallelopied are of unit length and are parallel ...
Text Solution
|
- Let hat(a), hat(b) and hat(c) be the non-coplanar unit vectors. The an...
Text Solution
|
- The edges of a parallelopiped are of unit length and are parallel to ...
Text Solution
|
- The edges of a parallelopiped are of unit length and are parallel to n...
Text Solution
|
- एक समानान्तर षट्फलक की कोरें एकांक लम्बाई की हैं तथा असमतलीय एकांक सदि...
Text Solution
|
- Let hat a , hat b ,and hat c be the non-coplanar unit vectors. The...
Text Solution
|
- If hat a , hat b ,"and " hat c are unit vectors, then | hat a+hat b|^...
Text Solution
|