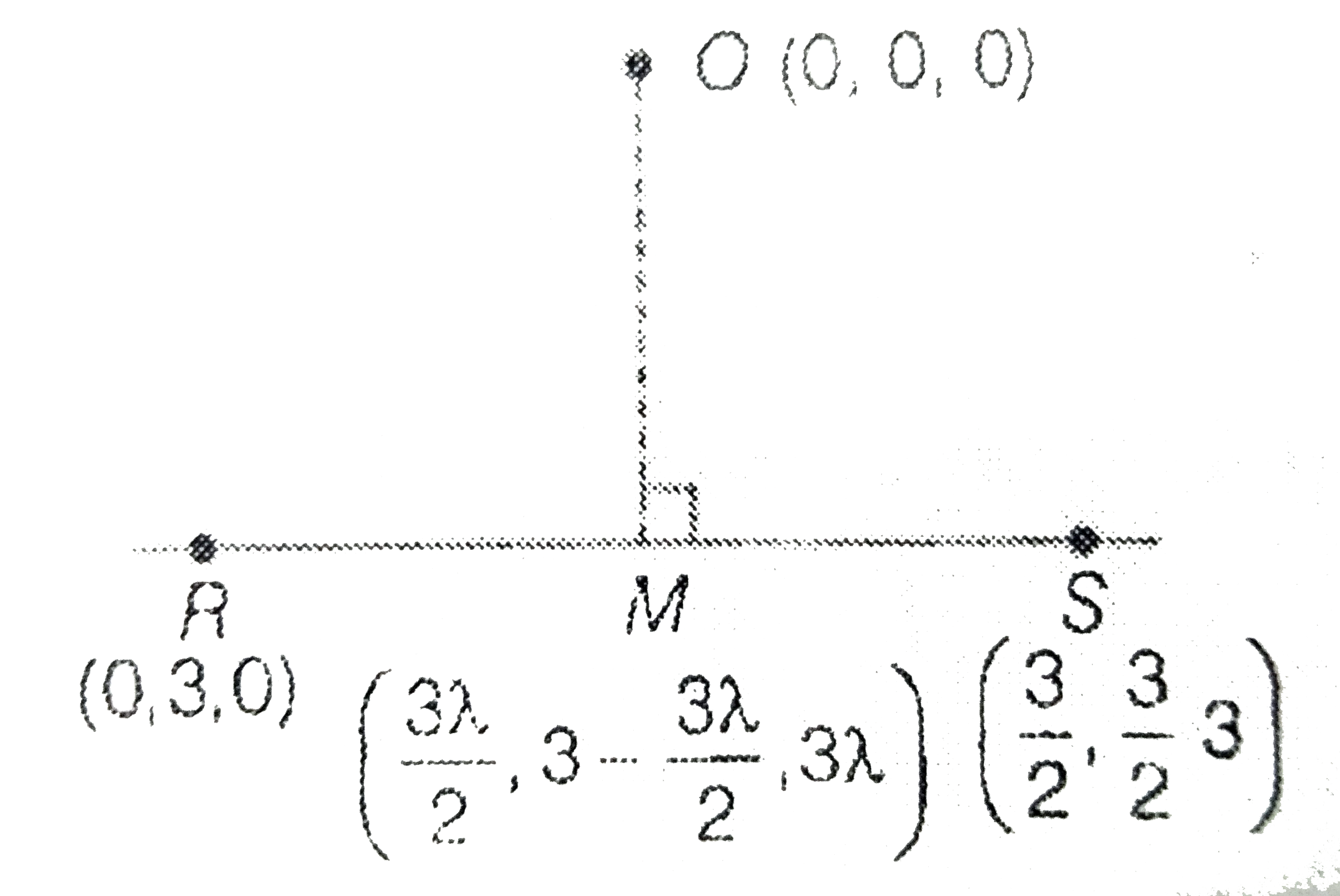A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
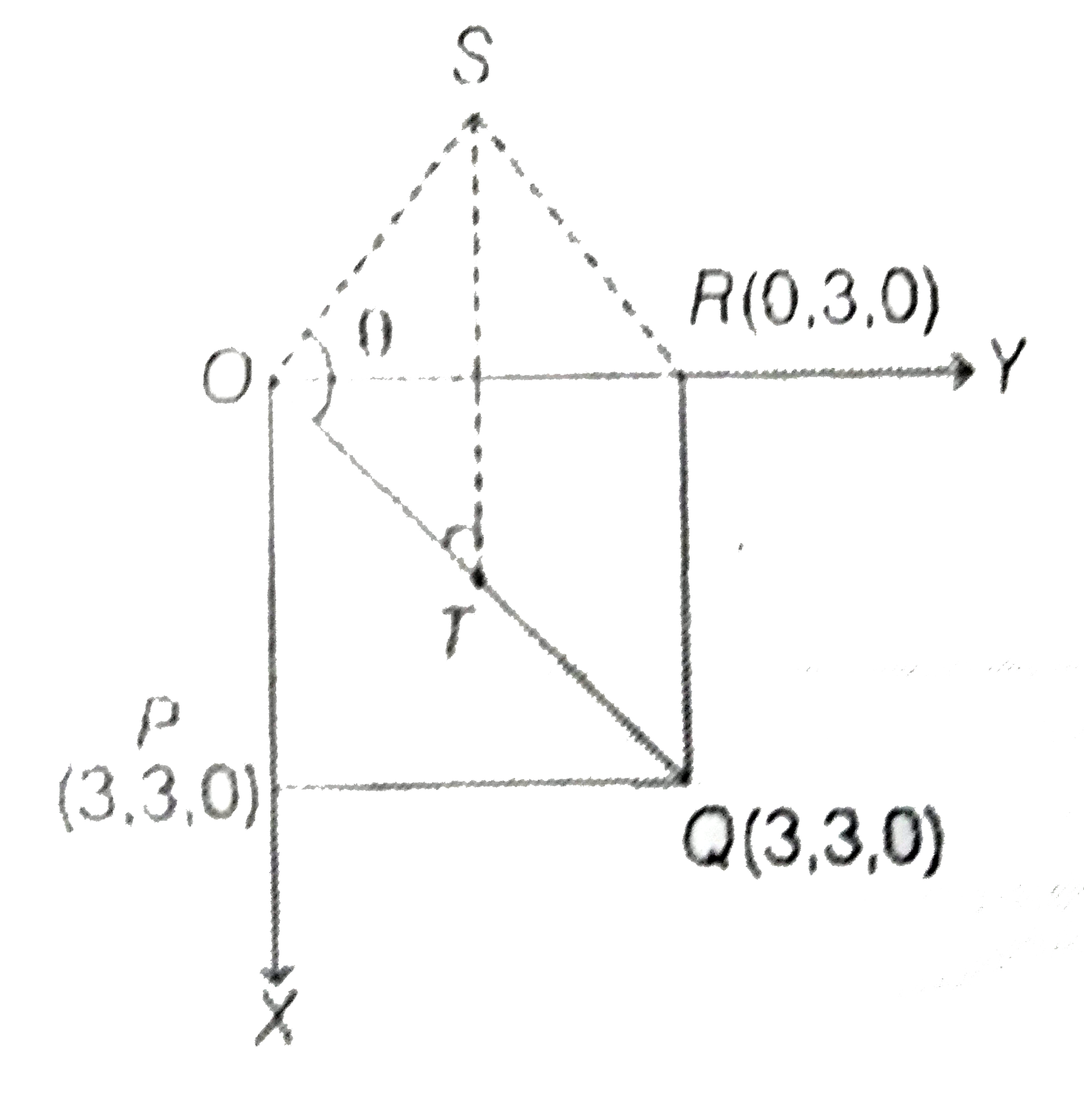
- Consider a pyramid OPQRS located in the first octant (x >= 0, y >= 0, ...
Text Solution
|
- P and Q are two points on the line x-y+1=0. If OP=OQ=6 then length of ...
Text Solution
|
- Consider a pyramid OPQRS located in the first octant (x >= 0, y >= 0, ...
Text Solution
|
- Consider a pyamid OPQRS locaated in the first octant ( x ge 0, y le 0...
Text Solution
|
- Consider a pyramid OPQRS located in the first octant (xge0, yge0, zge0...
Text Solution
|
- यदि बिन्दु P, x-अक्ष पर इस प्रकार स्थित है कि इसकी मूल बिन्दु ...
Text Solution
|
- माना की एक पिरामिड OPQRS प्रथम अष्टक (xge0,yge0)O मूलबिंदु के साथ स्थ...
Text Solution
|
- Consider a pyramid OPQRS located in the first octant (x ge 0, y ge 0, ...
Text Solution
|
- प्रथम अष्टांश में एक ऐसे घन पर विचार कीजिए, जिसकी भुजाओं OP, OQ और OR ...
Text Solution
|