Because we have particles, the magnitude of the gravitational force on particel 1 due to either of the other particles is given by Eq. 13-1 (`F = Gm_1m_2//r^2`). The direction of a gravitational force on partile 1 is toward the particle responsible for the force. We can use symmetry to eliminate unneeded calculations.
Calculations : For the magnitudes of the forces on partice 1,first note that particles 2 and 4 have equal masses and equal distance of r = 2a from particle 1. Thus, form Eq. 13-1, we find that
`F_(12) = F_14 =(Gm_1m_3)/((2a)^2) (13-9)`
Similarly, since particles 3 and 5 have equal masses and are both at distance r = a from particle 1, we find
`F_(13) = F_(15) = (Gm_1m_3)/(a^2)` (13-10)
We could now substicute known data into these two equations to evaluate the magnitude of the forces,indicate thedireactionof the fores on the free-body diagram of Fig. 13-5b,and then find the net force either (1) by resolving the vectors into x and y components, finding the net x andnet y components, and then vectorially combining tem or (2) by adding the vectors directly on a vector-capable calculator.
Instead, however, we shall make further use of the symmetry of the problem. First, we note that `vecF_(12) and vecF_(14)` are equal inmagnitude but opposite in direaction, thus, those forces cancel. Inspection of Fig. 13-5b and Eq. 13-10 reveals that the x components of `vecF_(13) and vecF_15` also cancel, and that their y components are identicalin magnitude and both act in the positive direaction of the y axis.
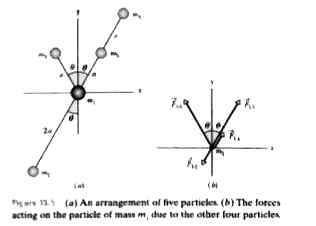
Figure 13-5 (a) An arrangement of five particles. (b) The forces acting on the particle of mass `m_1` due to the other four particles.
Thus, `vecF_("1.net")` acts in that same direction, and its magnitude is twice the y component of `vecF_(13)` :
`F_("1.net") = 2 F_(13) cos theta = 2(Gm_1m_3)/(a^2) costheta`
`=(2(6.67 xx 10^(-11)m^3//Kg.s^2)(8.0kg)(2.0kg))/((0.020m)^2)cos30^@`
`4.6 xx 10^(-6)N`.
Note: The presence of particle 5 along the line between partiicles 1 and 4 does not alter the gravitational force on particel 1 from particle 4.