A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
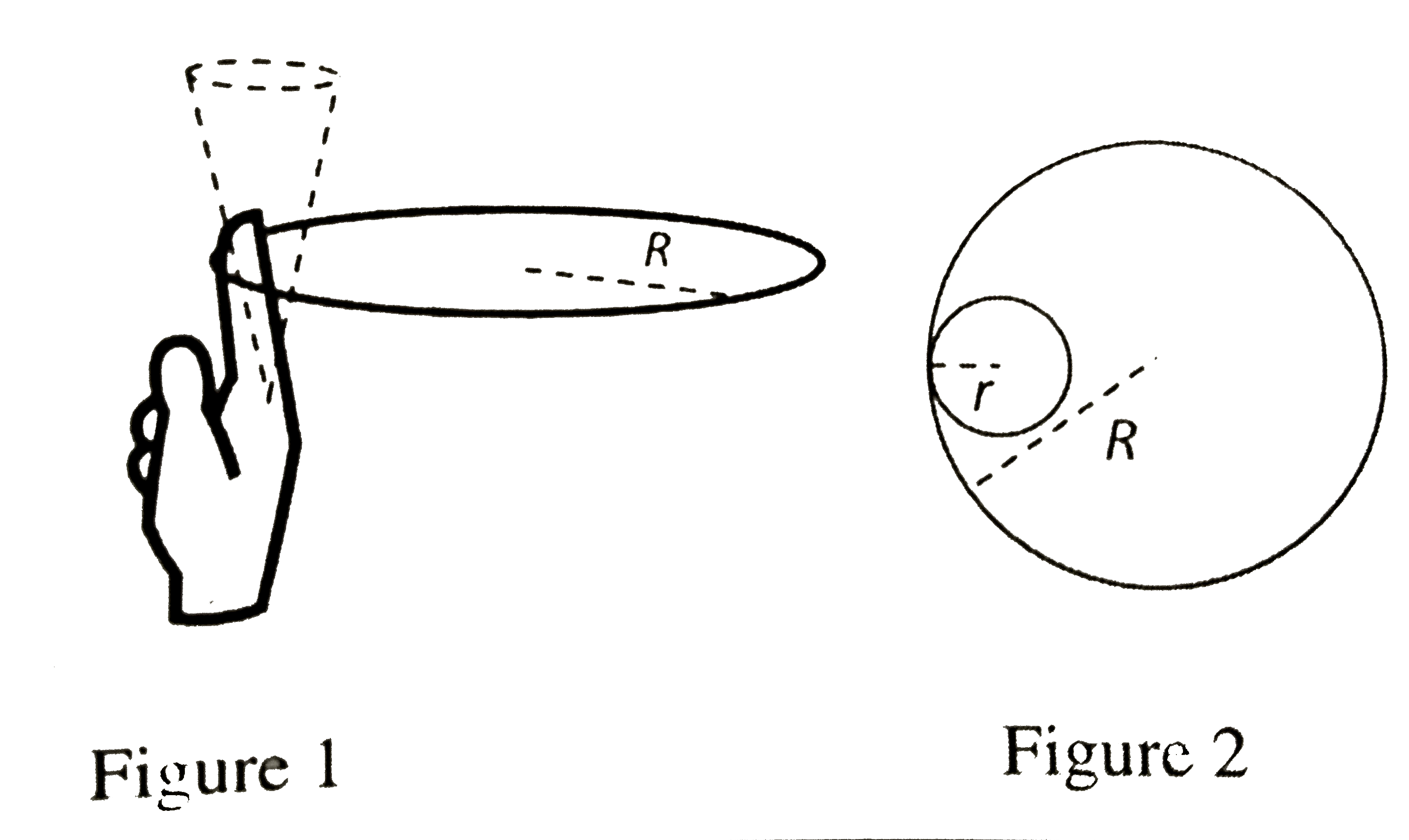
- One twirls a circular ring (of mass and radius ) near the tip of one’s...
Text Solution
|
- One twirls a circular ring (of mass and radius ) near the tip of one’s...
Text Solution
|
- In how many ways five different rings can be worn in four fingers with...
Text Solution
|
- In how many ways five different rings can be put on four fingers with ...
Text Solution
|
- यदि अंगूठे के लिए एक, तर्जनी (Index ) उँगली के लिए दो, मध्यमा (Middle)...
Text Solution
|
- There are 7 distinguishable rings. The number of possible five - rings...
Text Solution
|
- Given eight distinguishable rings, the number of possible five ring ar...
Text Solution
|
- एक वृत्ताकार वलय (circular ring)(द्रव्यमान M एवं त्रिज्या R) एक उंगली ...
Text Solution
|
- एक वृत्ताकार वलय (द्रव्यमान M एवं त्रिज्या R) एक उंगली के परितः धुतघूर...
Text Solution
|