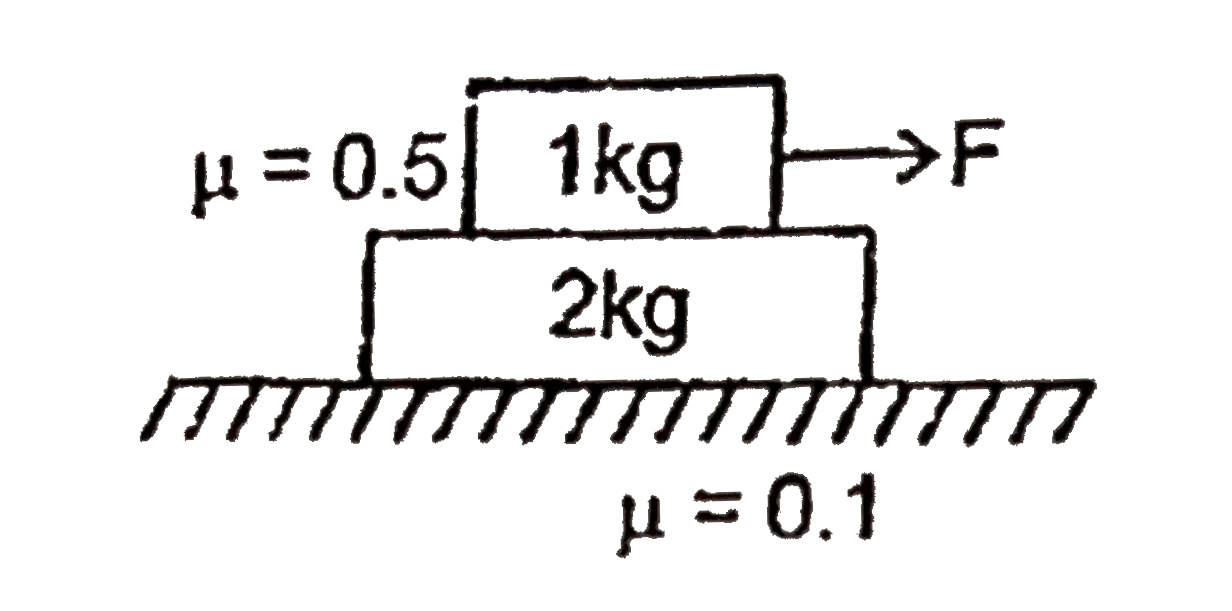Similar Questions
Explore conceptually related problems
Recommended Questions
- What should be minimum value of F so that 2 kg slides on ground but 1k...
Text Solution
|
- In the figure shown, the minimum force F to be applied perpendicular t...
Text Solution
|
- In given diagram what is the minimum value of a horizontal external fo...
Text Solution
|
- A block is rotating in contact with vertical wall (rotor) as shown. Fi...
Text Solution
|
- As shown in figure, if we apply a horizontal force F on the block, fin...
Text Solution
|
- In the figure, m(A)=2 kg and m(B)=4kg. For what minimum value of F,A s...
Text Solution
|
- Find the minimum value of F for which 5 kg being to slide if the coeff...
Text Solution
|
- What should be minimum value of F so that 2 kg slides on ground but 1k...
Text Solution
|
- A mass of 1 kg is just able to slide down the slope of a rough incline...
Text Solution
|