Similar Questions
Explore conceptually related problems
Recommended Questions
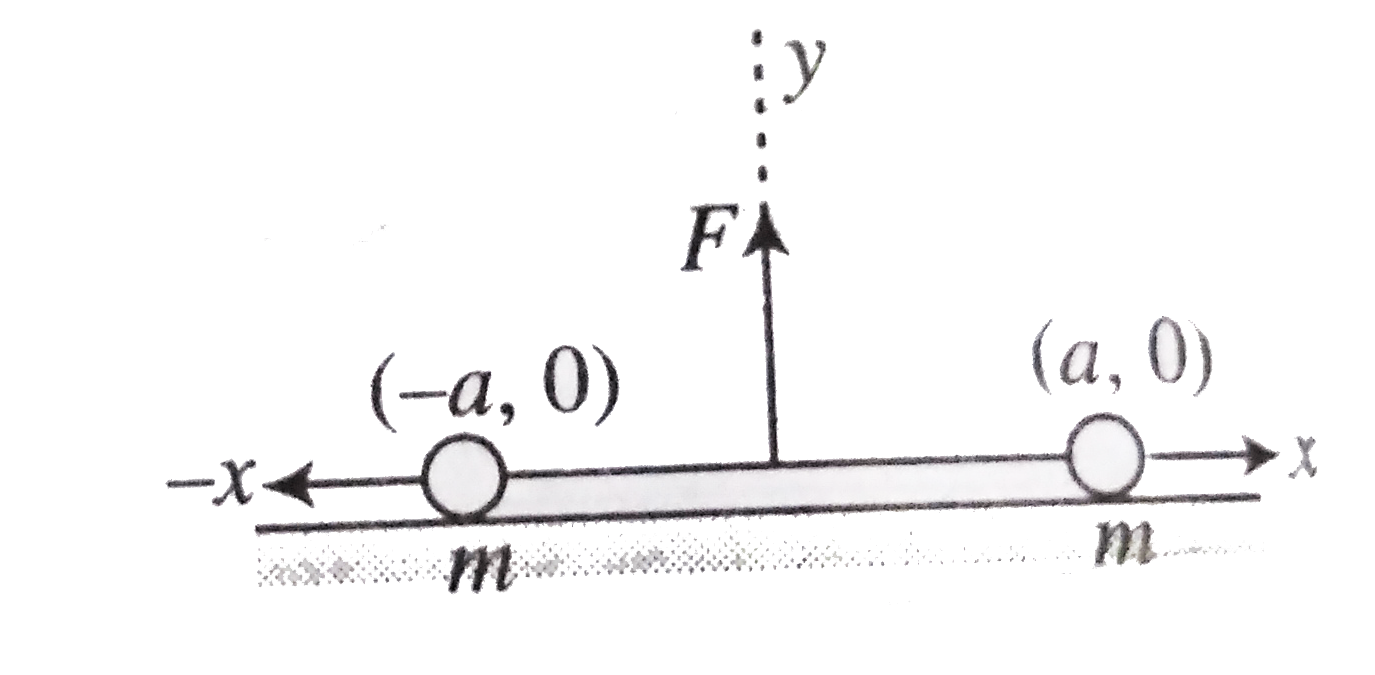
- Two masses each equal to m are lying on x-axis at (-a,0)(+a,0) respect...
Text Solution
|
- Two masses each equal to m are lying on x-axis at (-a,0)(+a,0) respect...
Text Solution
|
- Cube of mass m kept on rough horizontal surface. Two insects each mass...
Text Solution
|
- A 10 kg mass moves x-axis. Its acceleration as function of its positio...
Text Solution
|
- Two small particles P and Q each of mass m are fixed along x-axis at p...
Text Solution
|
- Two blocks of masses M and 2M are connected to each other through a ...
Text Solution
|
- A point object of mass m is kept at (a, 0) along x-axis. What mass sho...
Text Solution
|
- A large number of identical point masses m are placed along x - axis ,...
Text Solution
|
- Two point masses, each of mass 'm' are connected to the end of spring....
Text Solution
|