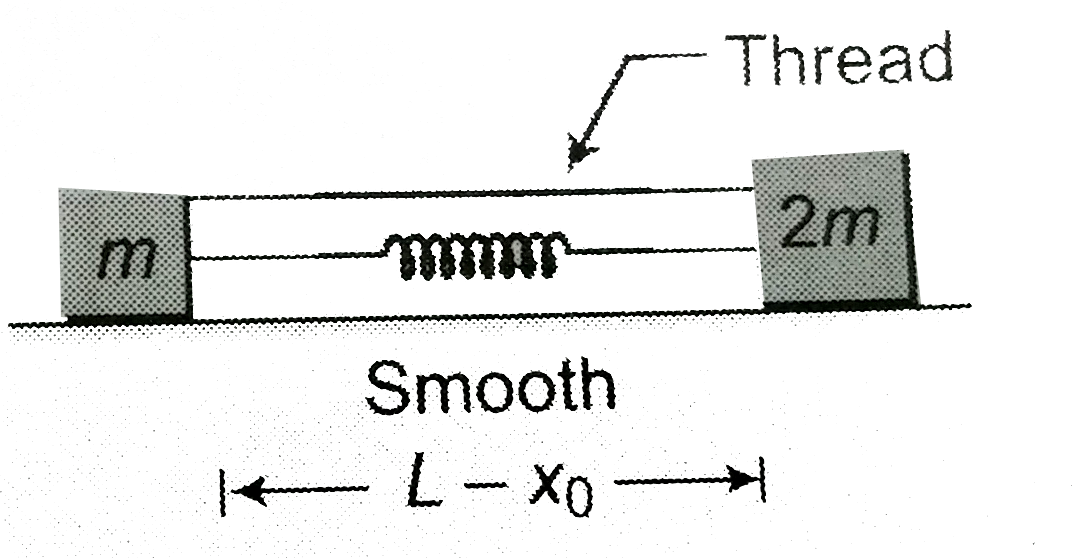Similar Questions
Explore conceptually related problems
Recommended Questions
- Two blocks of masses m and 2m compress a spring of spring constant k b...
Text Solution
|
- Two spring are connected toa block of mass M placed a frictionless sur...
Text Solution
|
- Two blocks of masses m and 2m rest on a frictionless horizontal surfac...
Text Solution
|
- A block of mass m moving at a speed v0 compresses a spring of spring c...
Text Solution
|
- Two blocks of masses m and 2m compress a spring of spring constant k b...
Text Solution
|
- Two identical blocks A and B , each of mass m resting on smooth floor ...
Text Solution
|
- In the figure shown the spring is compressed by 'x(0)' and released . ...
Text Solution
|
- A block of mass m connected to a spring of stiffness k is placed on ho...
Text Solution
|
- A block of mass m is placed on a smooth block of mass M = m with the h...
Text Solution
|