Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-THE ELEMENTS OF GEOMETRY -EXERCISE 3.1
- Answer the following: (i) How many dimensions a solid has? (ii) Ho...
Text Solution
|
- State whether the following statements are true or false? Also give re...
Text Solution
|
- In the figure given below, show that length AH gt AB + BC + CD.
Text Solution
|
- If a point Q lies between two points P and R such that PQ = QR, prove ...
Text Solution
|
- Draw an equilateral triangle whose sides are 5.2 cm. each
Text Solution
|
- What is a conjecture ? Give an example for it.
Text Solution
|
- Mark two points P and Q. Draw a line through P and Q. Now how many l...
Text Solution
|
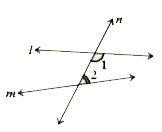
- In the adjacent figure, a line n falls on lines l and m such that the ...
Text Solution
|
- In the adjacent figures, If angle1 = angle3, angle2 = angle4 and angle...
Text Solution
|
- In the adjacent figure, we have BX = 1/2 AB, BY = 1/2 BC and AB=BC. Sh...
Text Solution
|