Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-LINES AND ANGLES -THINK, DISCUSS AND WRITE
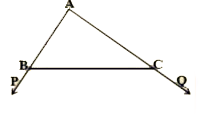
- In adjacent figure, sides AB and AC of DeltaABC are extended to points...
Text Solution
|
- What is the difference between intersecting lines and concurrent lines...
Text Solution
|
- Linear pair of angles are always supplementary. But supplementary angl...
Text Solution
|
- If the sides of a triangle are produced in order, what will be the sum...
Text Solution
|