Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-TRIANGLES -EXERCISE - 7.2
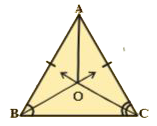
- In an isosceles triangle ABC, with AB = AC, the bisectors of / B and /...
Text Solution
|
- In DeltaABC, AD is the perpendicular bisector of BC (See adjacent figu...
Text Solution
|
- ABC is an isosceles triangle in which altitudes BD and CE are drawn to...
Text Solution
|
- ABC is a triangle in which altitudes BD and CE to sides AC and AB are ...
Text Solution
|
- DeltaABC and DeltaDBC are two isosceles triangles on thesame base BC (...
Text Solution
|