Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-AREAS -EXERCISE 11.3
- In a triangle ABC (see figure), E is the midpoint of median AD, show t...
Text Solution
|
- Show that the diagonals of a parallelogram divide it into four triangl...
Text Solution
|
- In the figure, ΔABC and ΔABD are two triangles on the same base AB. If...
Text Solution
|
- In the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB ...
Text Solution
|
- In the figure D, E are points on the sides AB and AC respectively of ...
Text Solution
|
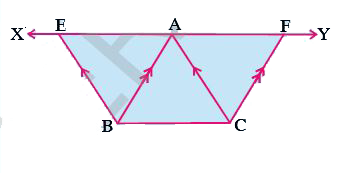
- In the figure, XY is a line parallel to BC is drawn through A. If BE |...
Text Solution
|
- In the figure, diagonals AC and BD of a trapezium ABCD with AB || DC i...
Text Solution
|
- In the figure, ABCDE is a pentagon. A line through B parallel to AC me...
Text Solution
|
- In the figure, if ar (DeltaRAS) = ar (DeltaRBS) and [ar (DeltaQRB) = a...
Text Solution
|