Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-SIMILAR TRIANGLES -TRY THIS
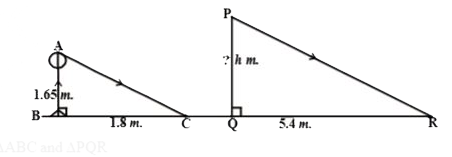
- A person 1.65m tall casts 1.8m shadow. At the same instance, a lamp p...
Text Solution
|
- In triangle Delta PQR, E and F are points on the sides PQ and PR respe...
Text Solution
|
- In triangle Delta PQR, E and F are points on the sides PQ and PR respe...
Text Solution
|
- In triangle Delta PQR, E and F are points on the sides PQ and PR respe...
Text Solution
|
- In the following figures DE || BC. (i) Find EC (ii) Find AD
Text Solution
|
- Are triangles formed in each figure similar? If so, name the criterio...
Text Solution
|
- If pairs of the triangles are similar and then find the value of x.
Text Solution
|