Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
TANGENTS AND SECANTS TO A CIRCLE
NCERT BANGLISH|Exercise Exercise (9.3)|8 VideosTANGENTS AND SECANTS TO A CIRCLE
NCERT BANGLISH|Exercise Optional exercise|7 VideosTANGENTS AND SECANTS TO A CIRCLE
NCERT BANGLISH|Exercise Exercise (9.1)|5 VideosSTATISTICS
NCERT BANGLISH|Exercise THINK AND DISCUSS|8 VideosTRIGONOMETRY
NCERT BANGLISH|Exercise OPTIONAL EXERCISE|6 Videos
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-TANGENTS AND SECANTS TO A CIRCLE-Exercise (9.2)
- Choose the correct answer and give justification for each. (i) The ...
Text Solution
|
- Choose the correct answer and give justification for each. (ii) Fro...
Text Solution
|
- Choose the correct answer and give justification for each. If AP an...
Text Solution
|
- Choose the correct answer and give justification for each. If tange...
Text Solution
|
- Choose the correct answer and give justification for each. In the f...
Text Solution
|
- Two concentric circles of radii 5cm and 3cm are drawn. Find the length...
Text Solution
|
- Prove that the parallelogram circumscibing a circle is a rhombus.
Text Solution
|
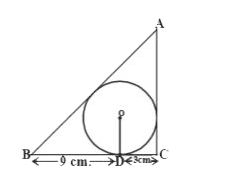
- A triangle ABC is drawn to circumscribe a circle of radius 3cm such th...
Text Solution
|
- Draw a circle of radius 6cm. From a point 10cm away its centre, constr...
Text Solution
|
- Construct a tangent to a circle of radius 4cm at any point .
Text Solution
|
- Draw a circle with the help of a compass. Take a point outside the cir...
Text Solution
|
- In a right triangle ABC, a circle with a side. AB as diameter is draw...
Text Solution
|
- Draw a circle with radius 4cm and draw a tangent at any point on the c...
Text Solution
|