Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
TANGENTS AND SECANTS TO A CIRCLE
NCERT BANGLISH|Exercise Optional exercise|7 VideosTANGENTS AND SECANTS TO A CIRCLE
NCERT BANGLISH|Exercise What we have discussed|6 VideosTANGENTS AND SECANTS TO A CIRCLE
NCERT BANGLISH|Exercise Exercise (9.2)|13 VideosSTATISTICS
NCERT BANGLISH|Exercise THINK AND DISCUSS|8 VideosTRIGONOMETRY
NCERT BANGLISH|Exercise OPTIONAL EXERCISE|6 Videos
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-TANGENTS AND SECANTS TO A CIRCLE-Exercise (9.3)
- Fill the blank: Atmost tangent can drawn from any point on the ci...
Text Solution
|
- In a circle of radius 12cm , a chord subtends an angle of 120^(@) at t...
Text Solution
|
- A car has two wipers which do not ovarlap. Each wiper has a blade of l...
Text Solution
|
- Find the area of the shaded region in the adjacent figure, where ABCD ...
Text Solution
|
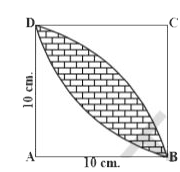
- Find the area of the shaded region in figure, if ABCD is a square of s...
Text Solution
|
- In the figure, OACB is a quadrant of a circle with centre O and radius...
Text Solution
|
- AB and CD are respectively arcs to two concentric circles of radii 21c...
Text Solution
|
- Calculate the area of the designed region in figure, common between th...
Text Solution
|