Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
RELATIONS AND FUNCTIONS
NCERT BANGLISH|Exercise MISCLELLANEOUS EXERCISE ON CHAPTER 1|19 VideosRELATIONS AND FUNCTIONS
NCERT BANGLISH|Exercise EXERCISE 1.3|14 VideosPROBABILITY
NCERT BANGLISH|Exercise MISCELLANEOUS EXERCISE ON CHAPTER 13|19 VideosVECTOR ALGEBRA
NCERT BANGLISH|Exercise Miscellaneous Exercise on chapter 10|19 Videos
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-RELATIONS AND FUNCTIONS -EXERCISE 1.4
- Let f(x+2)=3x -4,then find f^(-1) (1)
Text Solution
|
- For each opertion ** difined below, determine whether ** isw binary, c...
Text Solution
|
- Consider the binary opertion ^^ on the set {1,2,3,4,5} defined by a ^^...
Text Solution
|
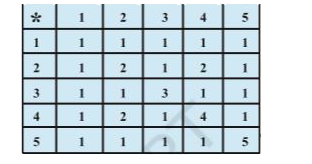
- Consider a binary opertion ** on the set {1,2,3,4,5} given by the foll...
Text Solution
|
- Consider the binary opertion ^^ on the set {1,2,3,4,5} defined by a ^^...
Text Solution
|
- Let ** be the binary opertion on N given by a **b=L.C.M. of a and b. F...
Text Solution
|
- Is ** defined on the set {1,2,3,4,5} by a ** b =L.C.M. of a and b a bi...
Text Solution
|
- Let ** be the binary opertion on N defined by a **b=H.C.F. of a and b....
Text Solution
|
- Let ** be a binary opertion on the set Q of rational numbers as follow...
Text Solution
|
- Let f(x+1)=2x -3,then find f^-1(x)
Text Solution
|
- Let A = N xx N and ** be the binary opertion on A defined by (a,b) ...
Text Solution
|
- State whether the following statements are true or false, Justify. ...
Text Solution
|
- Consider a binary opertion ** on N defined as a **b=a ^(3) +b ^(3). Ch...
Text Solution
|