Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT KANNAD-CIRCLES-EXERCISE 12.5
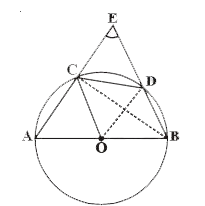
- In figure, bar(AB) is a diameter of the circle, bar(CD) is a chord equ...
Text Solution
|
- Given that the vertices A, B, C of a quadrilateral ABCD lie on a circl...
Text Solution
|
- Prove that a cyclic rhombus is a square
Text Solution
|
- For each of the following, draw a circle and inscribe the figure given...
Text Solution
|