Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
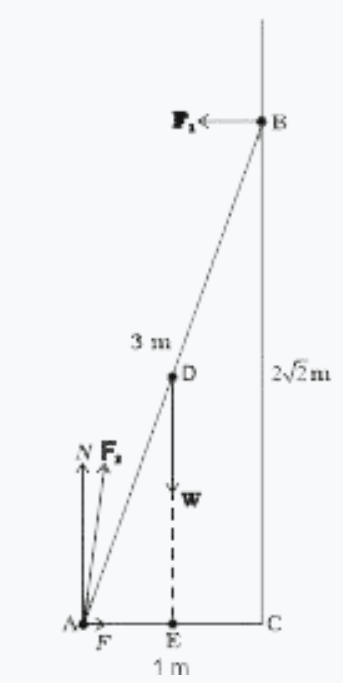
- A 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet...
Text Solution
|
- A uniform ladder of mass 10 kg leans against a smooth vertical wall ma...
Text Solution
|
- In the figure, a ladder of mass m is shown leaning against a wall. It ...
Text Solution
|
- A 3m along ladder weighing 20 kg leans on a frictionless wall. Its fee...
Text Solution
|
- 20 kg द्रव्यमान की एक3m लम्बी सीढ़ी एक घर्षणविहीन दीवार के साथ झुका क्...
Text Solution
|
- 20 किग्रा द्रव्यमान की एक 3 मी. लंबी सीढ़ी एक घर्षण विहीन दीवार के साथ...
Text Solution
|
- A 3 m long ladder weighing 20 kg leans on a frictionless wall. Its fee...
Text Solution
|
- A 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet...
Text Solution
|
- A 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet...
Text Solution
|