Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
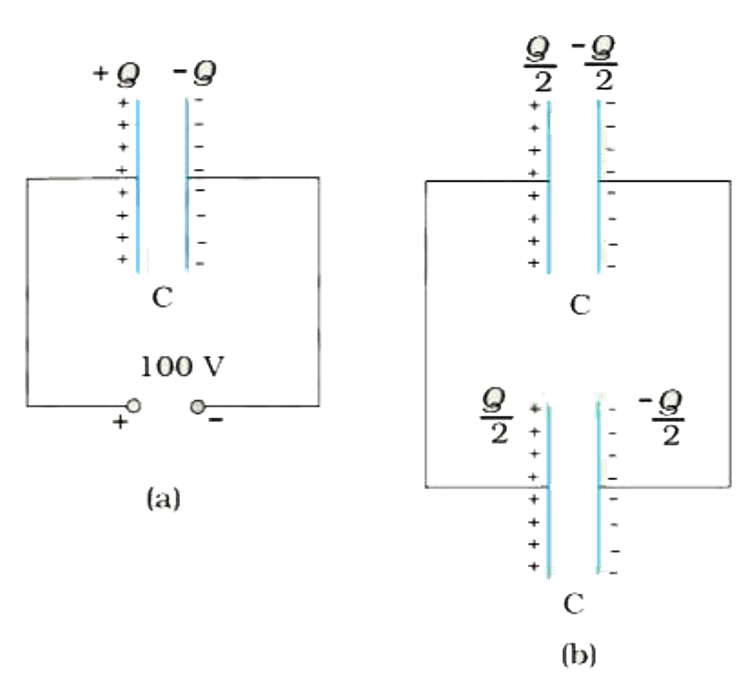
- (a) A 900 pF capacitor is charged by 100 V battery [Fig. 2.31(a)]. How...
Text Solution
|
- A 900 pF capacitor is charged by 100V battery. (a) How much electro...
Text Solution
|
- A 900pF capacitor is charged by 100 V battery. How much electros-tatic...
Text Solution
|
- A 900 pF capacitor is charged by 100V battery. (a) How much electro...
Text Solution
|
- A 900 pF capacitor is charged by a 100 V battery. How much electrostat...
Text Solution
|
- A 900 pF capacitor is charged by a 100 V battery. The capacitor is dis...
Text Solution
|
- A 900 pF capacitor is charged by a 100 V battery. The electrostatic en...
Text Solution
|
- (a) A 900 pF capacitor is charged by 100 V battery [Fig. 2.31(a)]. How...
Text Solution
|
- (a) A 900 pF capacitor is charged by 100 V battery [Fig. 2.31(a)]. How...
Text Solution
|