Home
Class 8
MATHS
An ant is moving around a few food piece...

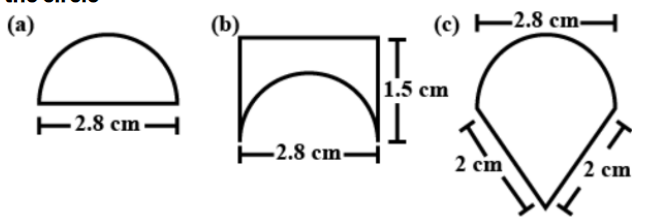
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression `c=2pir,` where r is the radius of the circle.

Text Solution

Verified by Experts

(a) Radius of the semicircle part=`(2.8/2)cm=1.4cm`
Perimeter of the circle= `2π`r
Perimeter of the semicircle =`pi r`
The perimeter of the food piece=`2.8cm+pi r`
`=2.8cm+(22/7xx1.4)cm`
`=5.8cmxx4.4cm`
`=10.2cm`
(b). Radius of semicircle part=`2.8/2=1.4cm`
...
Promotional Banner

Topper's Solved these Questions

  • MENSURATION

    NCERT|Exercise EXERCISE 11.4|8 Videos

  • MENSURATION

    NCERT|Exercise EXERCISE 11.3|10 Videos

  • LINEAR EQUATIONS IN ONE VARIABLE

    NCERT|Exercise EXERCISE 2.3|9 Videos

  • PLAYING WITH NUMBERS

    NCERT|Exercise SOLVED EXAMPLES|8 Videos

Similar Questions

Explore conceptually related problems

The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig. An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2piaE = d(phi)//dt , where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost. However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation, Centripetal force = magnetic force or mv^(2)//a = qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely epsilon = (d(phi)//dt) . Its energy after 'n' trips around the loop will be q(n(epsilon)) . Variable magnetic flux

The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig. An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2piaE = d(phi)//dt , where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost. However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation, Centripetal force = magnetic force or mv^(2)//a = qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely epsilon = (d(phi)//dt) . Its energy after 'n' trips around the loop will be q(n(epsilon)) . Working of betatron is not based upon which of the following theories?

A particle is moving in a circle of radious R with constant speed. The time period of the particle is T = 1s. In a time interval (T)/(6) , if the difference between average speed and the magnitude of average velocity of the particle is 2m/s, then report (49R)/(50) , where R is the radius of the circle (in metres) (take pi = 3.14 )

The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig. An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2piaE = d(phi)//dt , where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost. However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation, Centripetal force = magnetic force or mv^(2)//a = qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely epsilon = (d(phi)//dt) . Its energy after 'n' trips around the loop will be q(n(epsilon)) . Magnetic field which keeps the particles in circular path must

Let C_1, C_2, ,C_n be a sequence of concentric circle. The nth circle has the radius n and it has n openings. A points P starts travelling on the smallest circle C_1 and leaves it at an opening along the normal at the point of opening to reach the next circle C_2 . Then it moves on the second circle C_2 and leaves it likewise to reach the third circle C_3 and so on. Find the total number of different path in which the point can come out of nth circle.

(a) A uniform chain is lying in form of on arc of a circle of radius R. The arc subtends an angle of 2 alpha at the centre of the circle. Find the distance of the centre of mass of the chain from the centre of the circle. (b) A uniform chain of length (piR)/(2) is lying symmetrically on the top of a fixed smooth half cylinder (see figure) of radius R. The chain is pulled slightly from one side and released. It begins to slide. Find the speed of the chain when its one end just touches the floor. What is speed of centre of mass of the chain at this instant ? (c) In part (b) assume that the half cylinder is not fixed and can slide on the smooth floor. Find the displacement of the cylinder by the time one end of the chain touches the floor. Mass of cylinder is equal to that of the chain. For part (b) and (c) assume that the chain remains in contact with the cylinder all the while.

Using Rautherfold model of the atom, derive the expression for the total electron in hydrogen atom. What is the significance of total negative energy possedssed by the electron? Using Bohr's postulates of the atomic model, derive the expression for radius of n^(th) electron orbit. Hence obtain the expression for Bohr's radius This therory developed is applicable to Hydrogen atoms and ions having just one electron. Let us assume that the nucleus has a positive charge Ze (i.e. ther are Z protons in it) and electrons moves with a consant speed V along a circle of radius r with the centre at nucleus By Coulomb's law

Linked Comprehension Type Based upon each paragraph, three multiple choice questions have to be answered. Each question has four choices: a, b, c, and d, out of which only one is correct For Problems 1-3 center is at Each side of a square has length 4 units and its (3, 4). If one of the diagonals is parallel to the line y x, then answer the following questions 1. Which of the following is not the vertex of the square? a. (1, 6) b. (5, 2) c. (1, 2) d. (4, 6) 2. The radius of the circle inscribed in the triangle formed by any three vertices is a. 2020V2 1) 2012 1) d. none of these 3. The circle inscribed in the triangle forme radius of the by any two vertices of the square and the center is b. 202 1) a. 2012 1) d. none of these v2012 1) For Problems 4-6 Tangents PA and PB are drawn to the circle (x 4) 4 from the point P on the curve y sin x, where A and B on the circle. Consider the function y f(r) represented by locus of the center of the circumcircle of triangle PAB. T answer the following questions