Similar Questions
Explore conceptually related problems
Recommended Questions
- One of the forces acting on a certain particle depends on the particle...
Text Solution
|
- One of the forces acting on a certain particle depends on the particle...
Text Solution
|
- One of the forces acting on a certain particle depends on the particle...
Text Solution
|
- One of the forces acting on a certain particle depends on the particle...
Text Solution
|
- One of the forces acting on a certain particle depends on the particle...
Text Solution
|
- A particle of mass 2 kg moves in the xy plane under the action of a co...
Text Solution
|
- A force acting on a certain particle depends of the particles position...
Text Solution
|
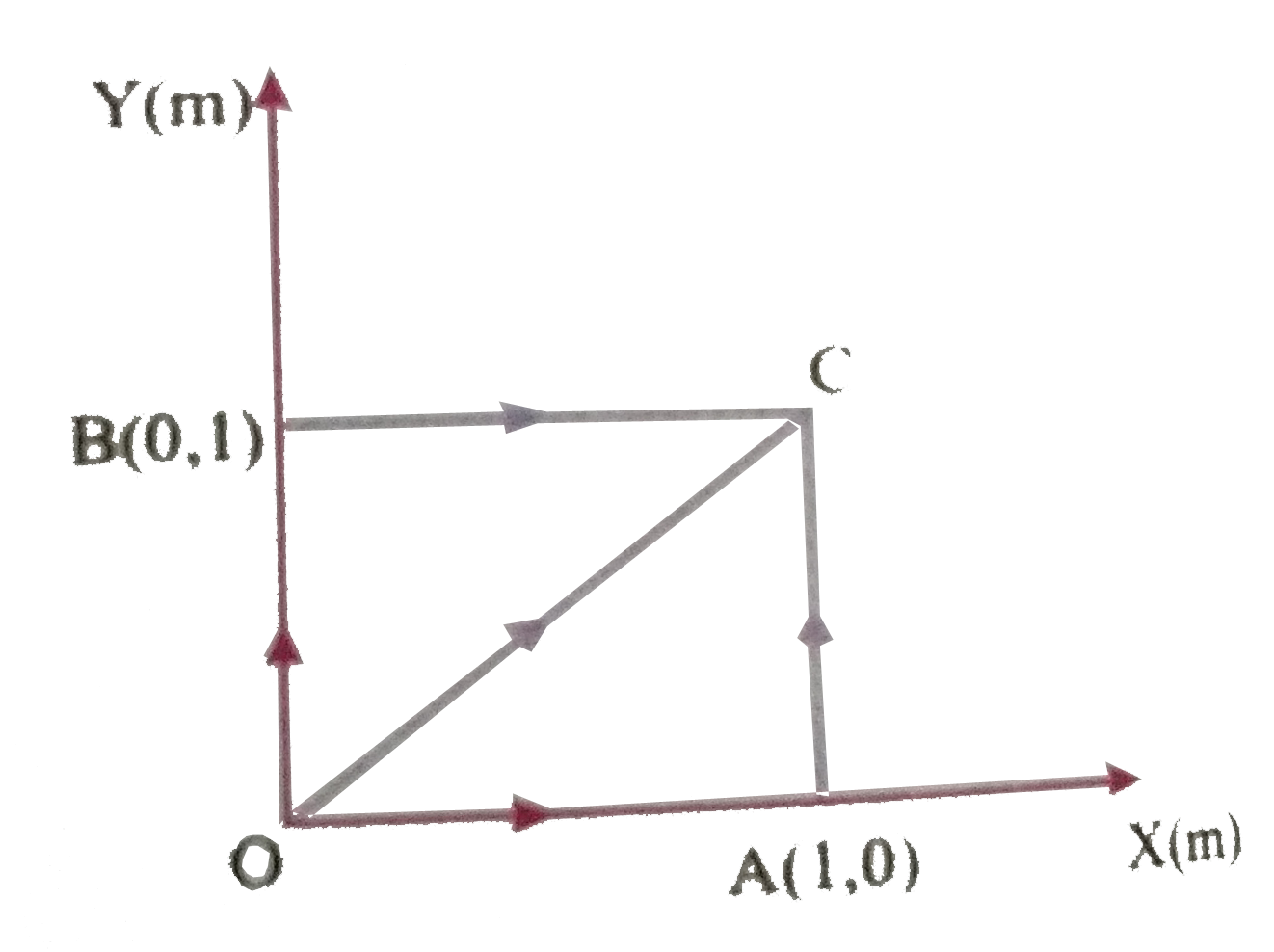
- A force F=-K(yhati+xhatj) (where K is a positive constant) acts on a p...
Text Solution
|
- A force F=-K(yhati+xhatj) (where K is a positive constant) acts on a p...
Text Solution
|