Similar Questions
Explore conceptually related problems
Recommended Questions
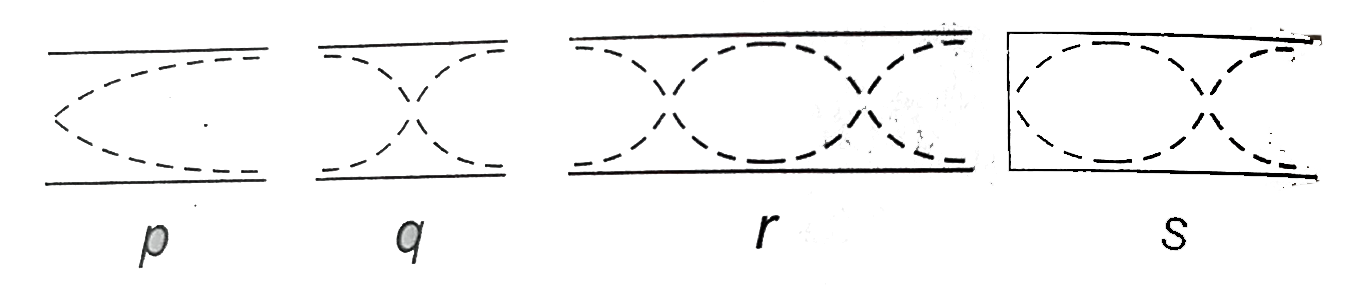
- The vibrations of four air columns are represented in the adjoining fi...
Text Solution
|
- Let n1ltn2ltn3ltn4ltn5 be positive integers such that n1+n2+n3+n4+n5="...
Text Solution
|
- The vibrations of four air columns are represented in the adjoining fi...
Text Solution
|
- A string A has double the length, double the tension, double the diame...
Text Solution
|
- Figures shows the vibrations of foue air columns. The ratio of frequen...
Text Solution
|
- किसी उच्चायी ट्रांसफॉर्मर के द्वितीयक में फोरों की सख्यां प्राथमिक ...
Text Solution
|
- Figures shows the vibrations of four air column. The ratio of frequenc...
Text Solution
|
- Two vibrating strings of the same material but lengths L and 2L have r...
Text Solution
|
- The vibrations of four air columns under identical conditions are repr...
Text Solution
|