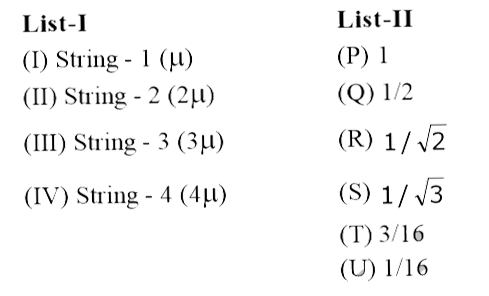Similar Questions
Explore conceptually related problems
Recommended Questions
- A musical instrument is made using four different metal strings, 1, 2,...
Text Solution
|
- A string tied between x = 0 and x = l vibrates in fundamental mode. Th...
Text Solution
|
- The frequency (f) of a stretched string depends upen the tension F (di...
Text Solution
|
- Length of string og musical instrument is varied from L(o) to 2L(o) in...
Text Solution
|
- The free length of all four string is varied from L(0) to 2L(0). Find ...
Text Solution
|
- The frequency f of vibration of a string between two fixed ends is pro...
Text Solution
|
- A string of mass per unit length mu is clamped at both ends such that ...
Text Solution
|
- Two strings of the same length but different mass per unit length are ...
Text Solution
|
- String-1 is connected with string-2 The mass per unit length in string...
Text Solution
|