Similar Questions
Explore conceptually related problems
Recommended Questions
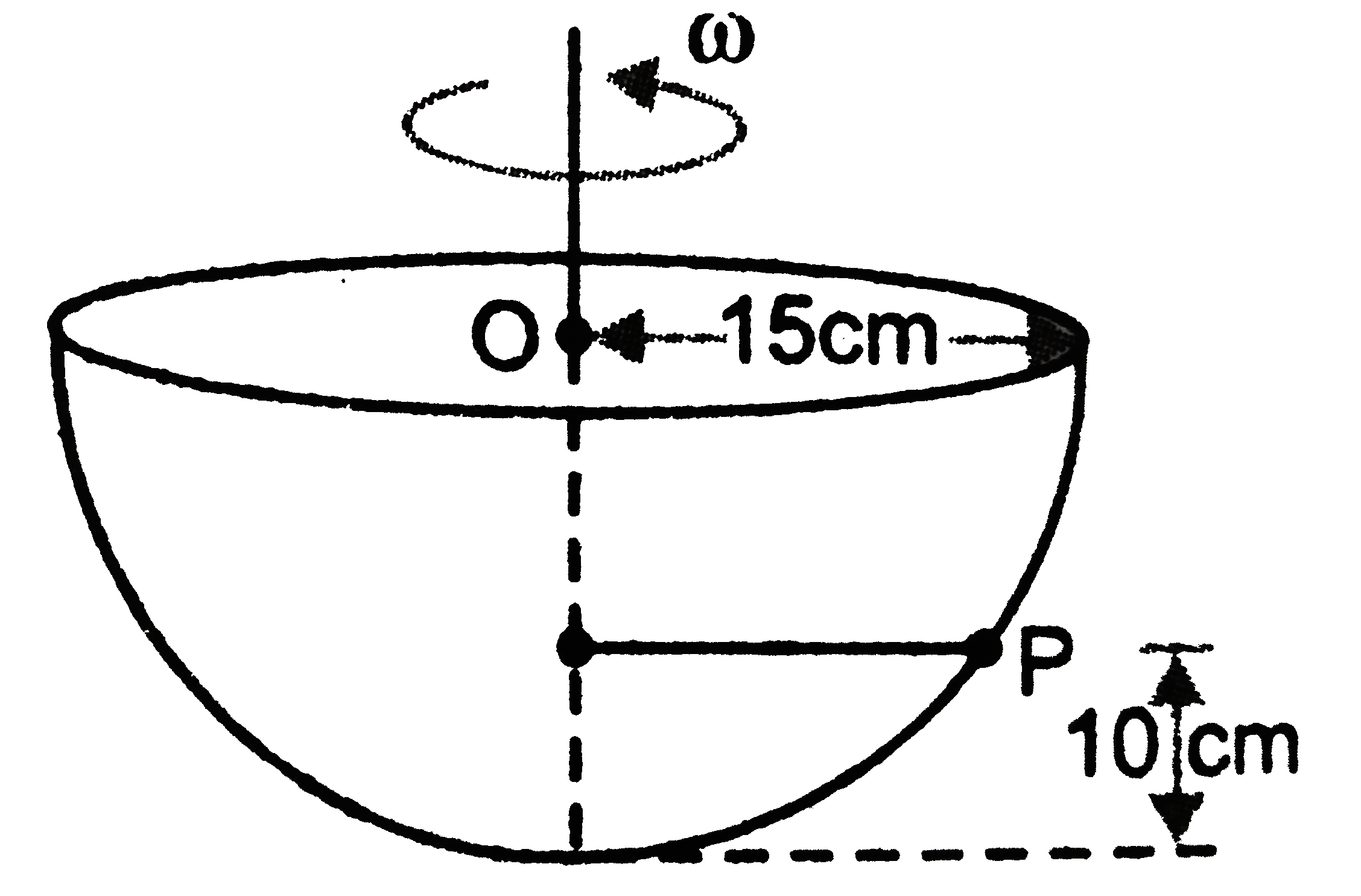
- A smooth hemispherical bowl 30 cm diameter potates with a constatn an...
Text Solution
|
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|
- A smooth hemispherical bowl 30 cm diameter, rotates with a constant a...
Text Solution
|
- A smooth hemispherical bowl 30 cm diameter potates with a constatn an...
Text Solution
|
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|
- A particle is placed inside a hemispherical bowl which rotates about i...
Text Solution
|
- A hemispherical bowl of radius 0.1m is rotated about a vertical axis p...
Text Solution
|
- एक शंक्वाकार प्याले के वृत्तीय आधार का व्यास 4 cm है तथा ऊँचाई 5 cm है...
Text Solution
|
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|
 .
.