Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- (a) Write an expression of magnetic moment associated with a current (...
Text Solution
|
- The magnetic field at the centre of a circular coil carrying current I...
Text Solution
|
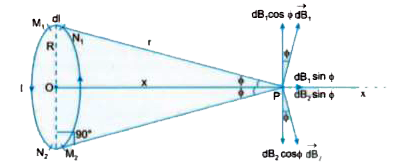
- Write the expression for the magnetic induction at any point on the ax...
Text Solution
|
- A circular coil of radius 'r' having N turns carries a current ''I''. ...
Text Solution
|
- A circular conducting coil of radius a and resistance R is placed with...
Text Solution
|
- A circular coil of closely wound N turns and radius r carries a curren...
Text Solution
|
- Write the expression for magnetic field at the centre of a current car...
Text Solution
|
- A circular coil with 100 turns and radius 20 cm is kept in Y-Z plane w...
Text Solution
|
- (a) Write an expression of magnetic moment associated with a current (...
Text Solution
|