Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
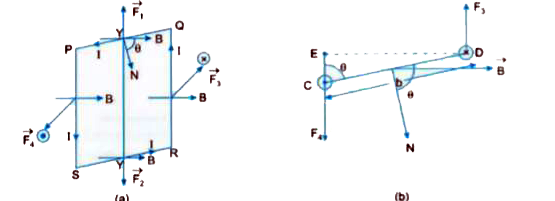
- (a) Derive the expression for the torque acting on the rectangular cur...
Text Solution
|
- If a particle of charge q is moving with velocity v along the y-axis a...
Text Solution
|
- A beam of alpha particles projected along + x-axis, experiences a forc...
Text Solution
|
- V वोल्ट विभवान्तर द्वारा त्वरति किये गये एक सरल रेखा में गति करते हुए ...
Text Solution
|
- a) Obtain the expression for the deflecting torque acting on the curre...
Text Solution
|
- A proton and an alpha particle accelerated through the same potential ...
Text Solution
|
- एकसमान चुम्बकीय क्षेत्र में प्रवेश करने वाले एल्फा कणों A और B के वेग ...
Text Solution
|
- In a region, a uniform electric field of 100V.m^(-1) is acting along x...
Text Solution
|
- A charge particle enters into a region containing uniform electric fie...
Text Solution
|