Similar Questions
Explore conceptually related problems
Recommended Questions
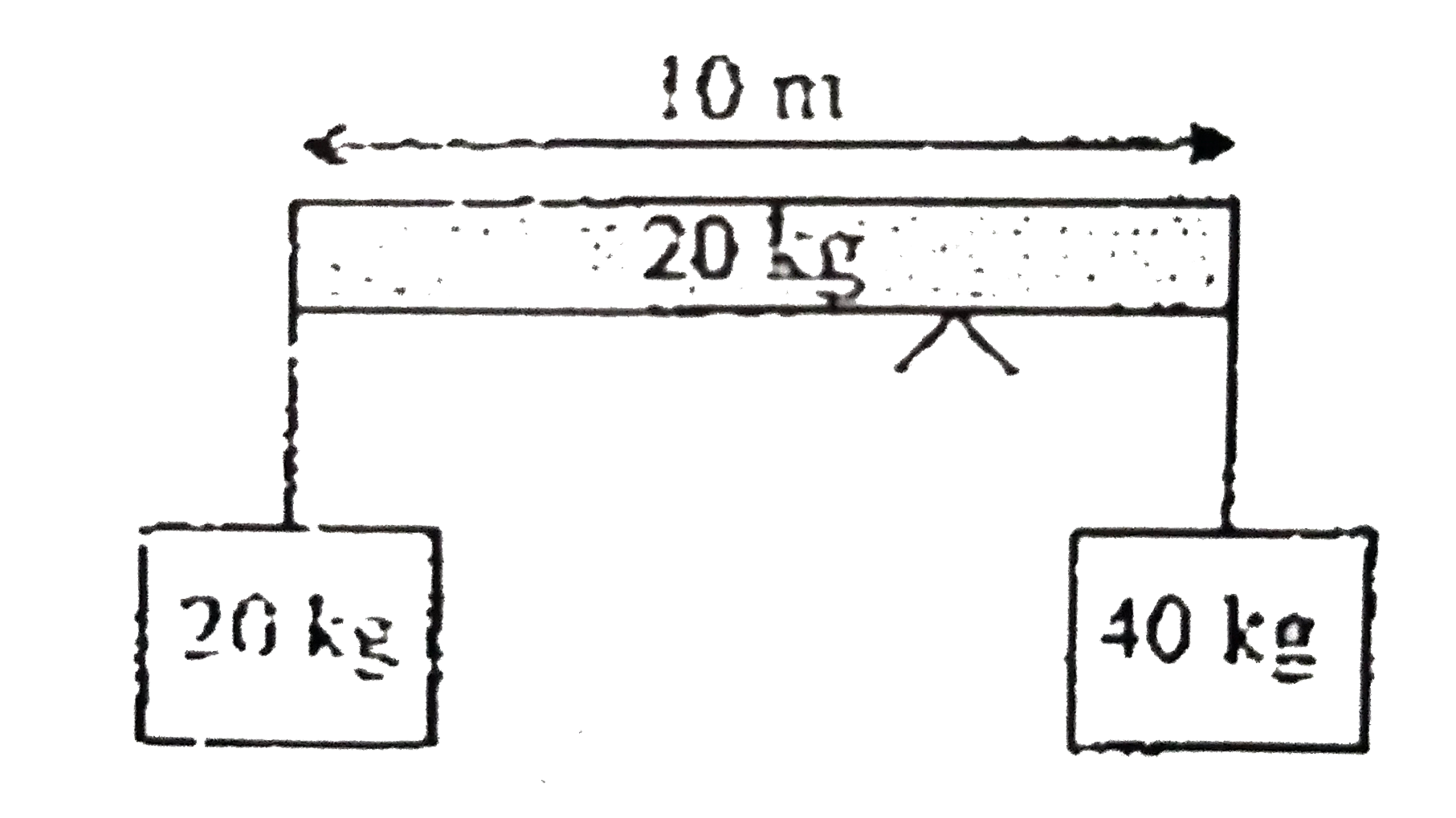
- A uniform rod of length 10meters and mass 20 kilograms is balanced on ...
Text Solution
|
- A mass m is at a distance a from one end of a uniform rod of length l ...
Text Solution
|
- As shown in the figure, two blocks, each of mass m, suspended from the...
Text Solution
|
- A uniform rod of length 10meters and mass 20 kilograms is balanced on ...
Text Solution
|
- The mass per unit length of a non-uniform rod of length L is given by ...
Text Solution
|
- एक हल्की छड़ की लम्बाई । है। इसके सिरों पर m1 " व् " m2 द्रव्यमान के ...
Text Solution
|
- किसी एकसमान छड़ के एक सिरे से उसके द्रव्यमान केन्द्र की स्थिति ज्ञात क...
Text Solution
|
- The mass per unit length of a non-uniform rod of length L is given by ...
Text Solution
|
- एक छड़ की लम्बाई 3 मीटर है तथा इसकी प्रति मीटर लम्बाई का द्रव्यमान एक...
Text Solution
|