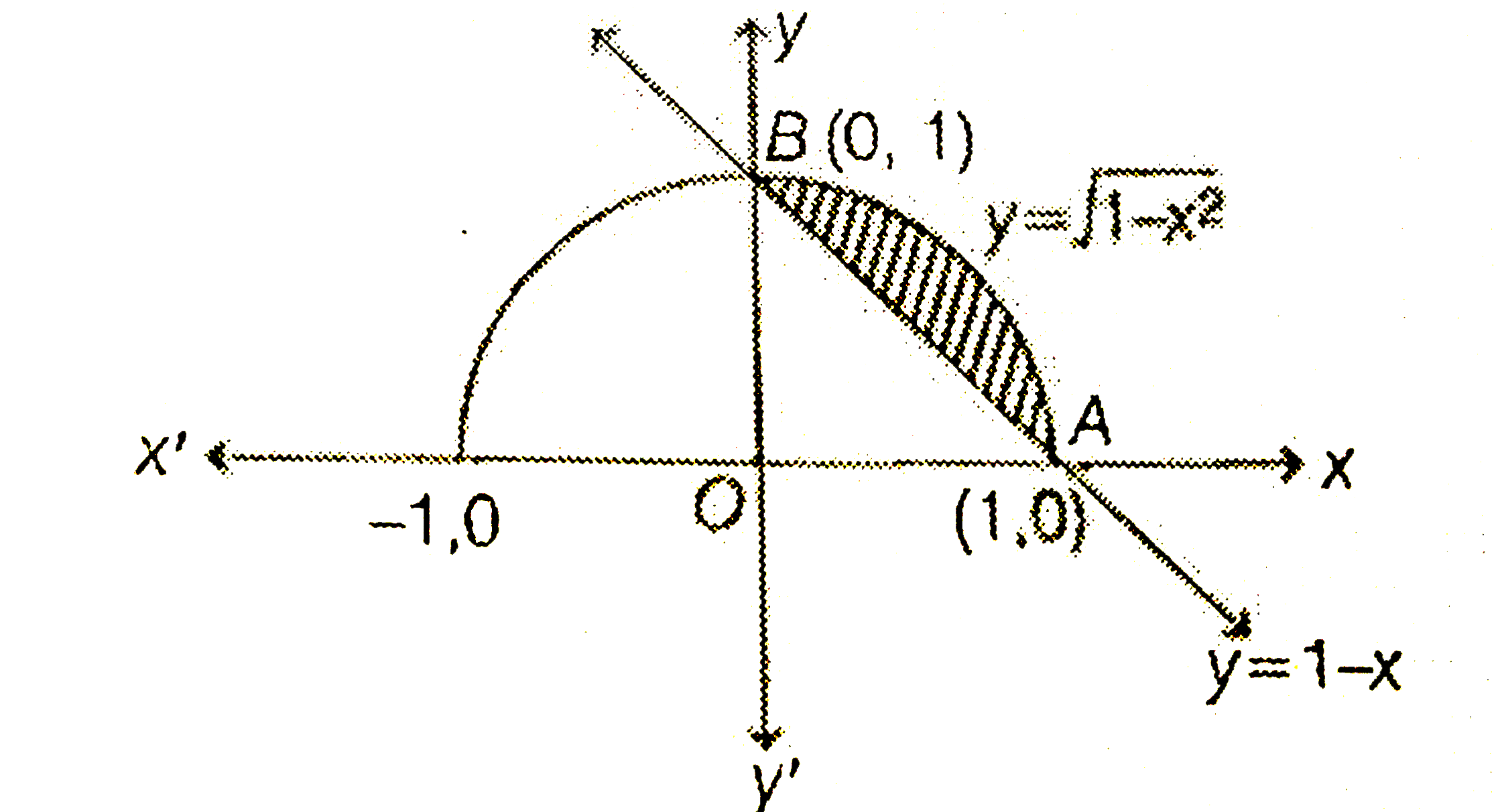
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let f:[0,\ oo)->R be a continuous function such that f(x)=1-2x+int0^...
Text Solution
|
- Let f:[0,oo)vecR be a continuous strictly increasing function, such th...
Text Solution
|
- Let f:(0,oo)vecR be given by f(x)=int(1/x)^x(e^(-(t+1/t))dt)/t , the...
Text Solution
|
- Let f:[0,oo)rarrR be a continuous function such that f(x)=1-2x+int(0)^...
Text Solution
|
- Let f:(0,oo) in R be given f(x)=int(1//x)^(x) e^-(t+(1)/(t))(1)/(t)d...
Text Solution
|
- Consider the function f:(-oo, oo) -> (-oo ,oo) defined by f(x) =(x^2...
Text Solution
|
- Consider the function f : (-oo , oo) to (-oo , oo) defined by f(x) = (...
Text Solution
|
- Let f be a continuous function on (0,oo) and satisfying f(x)=(log(e)x)...
Text Solution
|
- Let f:R ->(0,oo) be a real valued function satisfying int0^x tf(x-...
Text Solution
|