Home
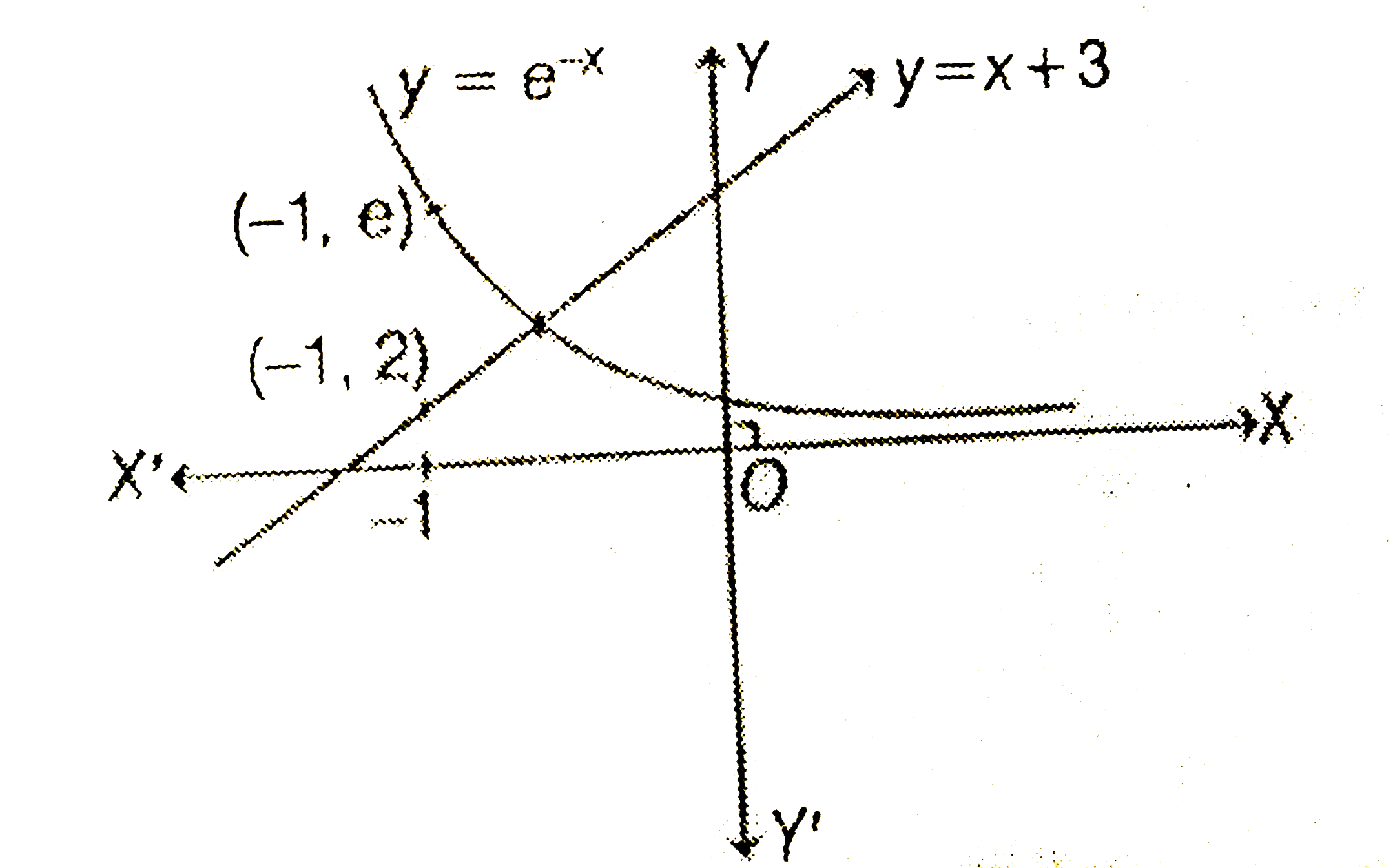
Class 12
MATHS
Let y(x) be a solution of the differen...

Let `y(x)` be a solution of the differential equation `(1+e^x)y^(prime)+y e^x=1.` If `y(0)=2` , then which of the following statements is (are) true?

A

`Y(-4) =0`

B

`Y(-2)=0`

C

y(x) has a critical point in the intervel (-1,0)

D

y(x) has no critical point in the interval (-1,0)

Text Solution

Verified by Experts

The correct Answer is:
A,C
Here, `(1+e^(x))y'+ye^(x)=1`
`rArr dy/dx+ e^(x) cdotdy/dx+ye^(x)=1`
`rArr dy+e^(x)dy+ye^(x)dx=dx`
`rArr dy+d(e^(x)y)=dx`
On integrating voth sides, we get
`y+e^(x)y=x+C`
Given, `y(0)=2`
`rArr 2+e^(0) cdot 2=0+C`
`rArr C =4`
`therefore y(1+e^(x))=x+4`
`rArr y=(x+4)/(1+e^(x)`
Now at `x=-4, y=(-4+4)/(1+e^(-4))=0`
`therefore y(-4)=0 ... (i)`
For critical points, `dy/dx= 0`
i.e. `dy/dx=((1+e^(x)) cdot1-(x+4)e^(x))/((1+e^(x))^(2))=0`
`rArr e^(x) (x+3)-1=0`
or `e^(-x)=(x+3)`
Clearly, the intersection point lies between (-1,0).
`therefore y(x)` has a critical point in the interval (-1,0).
Promotional Banner

Similar Questions

Explore conceptually related problems

Let y(x) be a solution of the differential eqution (1 +e^x)y' +ye^x = 1. If y(0) =2, then which of the following statements is (are) true?

The solution of the differential equation e^(x)dx+e^(y)dy=0 is

The solution of the differential equation e^(x)dx+e^(y)dy=0 is

Solution of the differential equation (x-y)(1-(dy)/(dx))=e^(x) is

The solution of the differential equation x(e^(2y)-1)dy + (x^2-1) e^y dx=0 is

Let y(x) be the solution of the differential equation 2x^2dy + (e^y-2x)dx = 0, x>0. If y(e) = 1, then y(1) is equal to :

what is the solution of the differential equation (dy)/(dx)=e^(x-y) (e^(y-x) -e^(y)) ?

The solution of the differential equation (dy)/(dx) = e^(3x-2y) +x^(2)e^(-2y) ,is