Similar Questions
Explore conceptually related problems
Recommended Questions
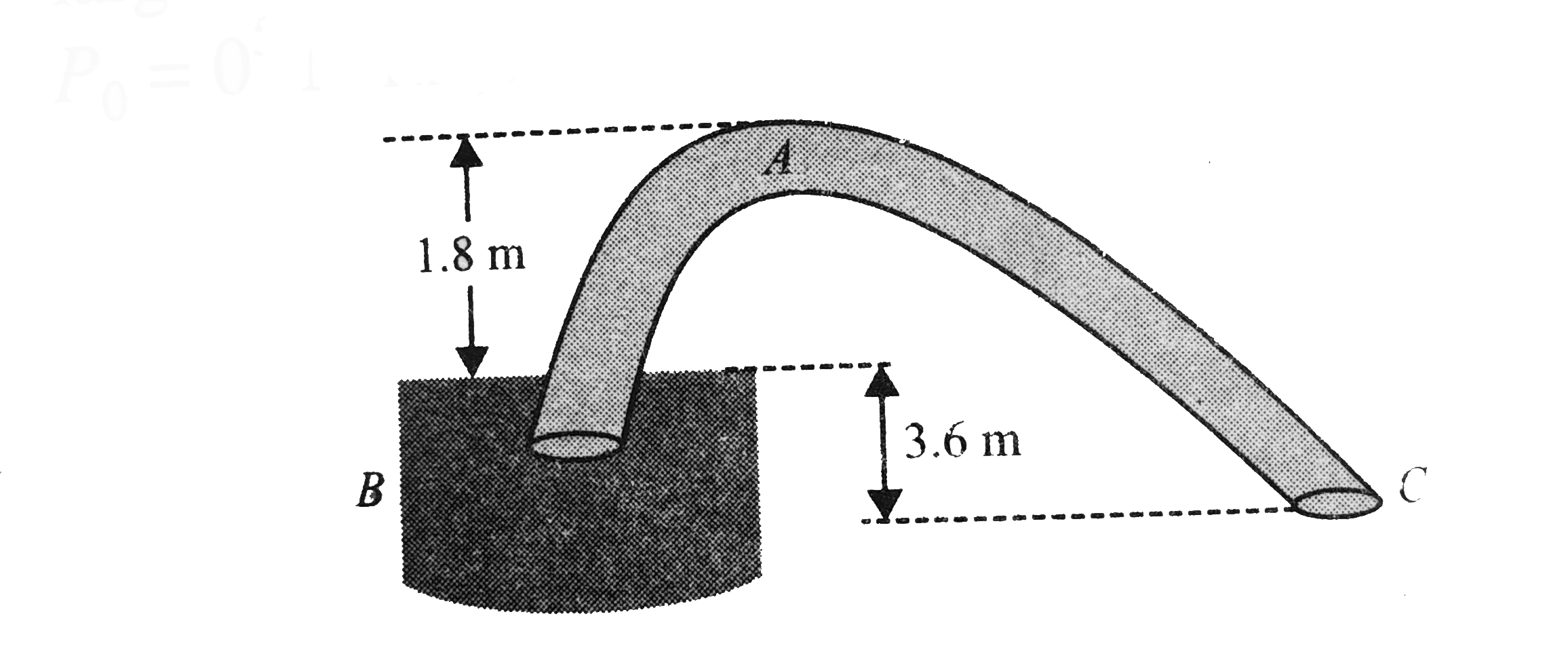
- A siphon has a uniform circular base of diameter 8//sqrt(pi) cm with i...
Text Solution
|
- The U-tube acts as a water siphon. The bend in the tube is 1m above th...
Text Solution
|
- A glass capillary tube (closed from tap) of inner diameter 0.28mm is l...
Text Solution
|
- A cylindrical vessel of a very large cross sectional area is containin...
Text Solution
|
- A siphon has a uniform circular base of diameter 8//sqrt(pi) cm with i...
Text Solution
|
- A tube of uniform cross section is used to siphon water from a vessel ...
Text Solution
|
- A tube of uniform cross section is used to siphon water from a vessel ...
Text Solution
|
- A glass capillary tube of inner diameter 0.28 mm is lowered vertically...
Text Solution
|
- A tube of small uniform cross section is used to siphon the water from...
Text Solution
|