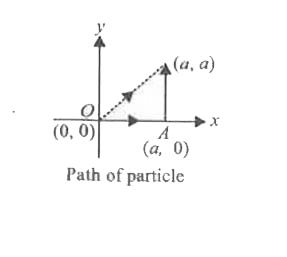Home
Class 12
PHYSICS
A force F=-K(yhati+xhatj) (where K is a ...

A force `F=-K(yhati+xhatj)` (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point `(a, 0)`, and then parallel to the y-axis to the point `(a, a)`. The total work done by the force F on the particle is

A

`-2 ka^(2)`

B

`2 ka^(2)`

C

`-ka^(2)`

D

`ka^(2)`.

Text Solution

Verified by Experts

The correct Answer is:
C
Total work done `=int_((0,0))^((a,a)) bar(F) .d overset(to)r`
`=int_((0,0))^((a,a))[-k(y overset(^)(i) + x overset(^)(j))]. [d x overset(^)(i) + d yoverset(^)(j)]`
`=int_((0,0))^((a,a))-k (ydx + xdy)`
`=int_((0,0))^((a,a)) -kd(xy)`
`=[-kxy]_((0,0))^((a,a))`
`therefore W=- ka^(2)`
Promotional Banner

Topper's Solved these Questions

  • WORK, POWER, ENERGY

    MTG-WBJEE|Exercise EXERCISE (WB JEE WORKOUT) CATEGORY 2 : Single Option Correct Type (2 Mark)|15 Videos

  • WORK, POWER, ENERGY

    MTG-WBJEE|Exercise EXERCISE (WB JEE WORKOUT) CATEGORY 3 : One or More than One Option Correct Type (2 Marks)|10 Videos

  • WAVE OPTICS

    MTG-WBJEE|Exercise WB JEE PREVIOUS YEARS QUESTION (MCQ.s)|9 Videos

Similar Questions

Explore conceptually related problems

A force vec(F) = - K (y hat(i) + x hat(j)) (where K is a positive constant) acts on a particle moving in the x - y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a, 0) and then parallel to the y-axis to the point (a, a) . The total work.done by the force F on the particle is:

A force vec((F)) = - K(yhat(i) + x hat(j)) (where K is a positive constant) acts on a particle moving in the X-Y plane. Starting from the origin, the particle is taken along the positive X-axis to the point (a, 0) and then parallel to the Y-axis to the point (a,a). The total done by the force vec(F) . of the particle is

A force vecF(yhatl+xhatJ), where K is a positive constant, acts on a particle moving in the XY-Plane. Starting from the origin, the particle is taken along the positive X-axis to a point (a,0) and then parallel to the y-axis to the point (a,a). Calculate the total work done by the force on the particle.

A force F = -K(y hatI + x hatj) (where K is a posive constant ) acts on a particle moving in the xy plane . Starting form the original , the partical is taken along in the positive x axis to the point (x,0) and then partical to they axis the point (x,0) . The total work done by the force F on the particls is

A force vecF=(4hati+5hatj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is

A force vecF=k[yhati+xhatj] where k is a positive constant acts on a particle moving in x-y plane starting from the point (3, 5), the particle is taken along a straight line to (5, 7). The work done by the force is :

A force vec F = (3 vec i + 4vec j)N , acts on a particle moving in x-y plane. Starting from origin, the particle first goes along x-axis to thepoint (4,0)m and then parallel to the y -axis to the point(4, 3)m. The total work done by the force on the particle is (##NAR_NEET_PHY_XI_P2_C06_E09_014_Q01.png" width="80%">

A single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is

A force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from